题目内容
在边长为1的等边△ABC中,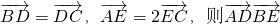 的值为________.
的值为________.
-
分析:根据△ABC是边长为1的等边三角形,可得 •
• =|
=| |•|
|•| |cos60°=
|cos60°= .再将向量
.再将向量 、
、 表示成
表示成 、
、 的线性组合,代入数据即可算出
的线性组合,代入数据即可算出 •
• 的值.
的值.
解答: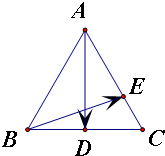 ∵
∵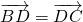 ,∴
,∴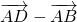 =
=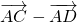 ,可得
,可得 =
= (
( )
)
又∵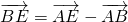 ,
,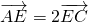
∴ =
=
 -
-
∵△ABC是边长为1的等边三角形
∴| |=|
|=| |=1,且
|=1,且 •
• =|
=| |•|
|•| |cos60°=
|cos60°=
因此, •
• =
= (
( )(
)(
 -
- )
)
=
 -
-
 •
• -
-
 =
= ×12-
×12- ×
× -
- ×12=-
×12=-
故答案为:-
点评:本题给出正三角形的中线和一边的三等分点,求向量的数量积,着重考查了正三角形的性质和平面向量数量积的运算等知识,属于基础题.

分析:根据△ABC是边长为1的等边三角形,可得
 •
• =|
=| |•|
|•| |cos60°=
|cos60°= .再将向量
.再将向量 、
、 表示成
表示成 、
、 的线性组合,代入数据即可算出
的线性组合,代入数据即可算出 •
• 的值.
的值.解答:
 ∵
∵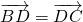 ,∴
,∴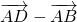 =
=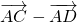 ,可得
,可得 =
= (
( )
)又∵
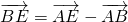 ,
,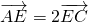
∴
 =
=
 -
-
∵△ABC是边长为1的等边三角形
∴|
 |=|
|=| |=1,且
|=1,且 •
• =|
=| |•|
|•| |cos60°=
|cos60°=
因此,
 •
• =
= (
( )(
)(
 -
- )
)=

 -
-
 •
• -
-
 =
= ×12-
×12- ×
× -
- ×12=-
×12=-
故答案为:-

点评:本题给出正三角形的中线和一边的三等分点,求向量的数量积,着重考查了正三角形的性质和平面向量数量积的运算等知识,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
在边长为1的等边△ABC中,设
=
,
=
,
=
,则
•
+
•
+
•
=( )
| BC |
| a |
| CA |
| b |
| AB |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
A、-
| ||
| B、0 | ||
C、
| ||
| D、3 |
在边长为1的等边△ABC中,设
=
,
=
,则
•
=( )
| BC |
| a |
| CA |
| b |
| a |
| b |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
 在边长为1的等边三角形ABC中,设
在边长为1的等边三角形ABC中,设| BC |
| a |
| CA |
| b |
| AB |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
A、
| ||
B、-
| ||
| C、0 | ||
| D、3 |
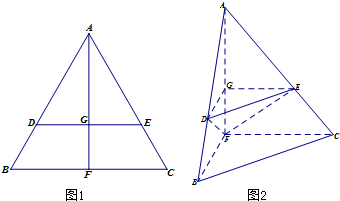 (2013•广东)如图1,在边长为1的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图2所示的三棱锥A-BCF,其中
(2013•广东)如图1,在边长为1的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图2所示的三棱锥A-BCF,其中