题目内容
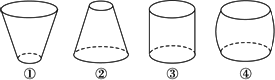
3、如图所示,向高为H的水瓶A,B,C,D同时以等速注水,注满为止;

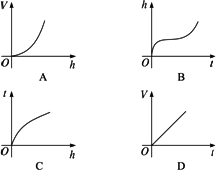
(1)若水深h与注水时间t的函数图象是下图中的a,则水瓶的形状是
(2)若水量v与水深h的函数图象是下图中的b,则水瓶的形状是
(3)若水深h与注水时间t的函数图象是下图中的c,则水瓶的形状是
(4)若注水时间t与水深20g的函数图象是下图中的d,则水瓶的形状是


(1)若水深h与注水时间t的函数图象是下图中的a,则水瓶的形状是
C
;(2)若水量v与水深h的函数图象是下图中的b,则水瓶的形状是
A
;(3)若水深h与注水时间t的函数图象是下图中的c,则水瓶的形状是
D
;(4)若注水时间t与水深20g的函数图象是下图中的d,则水瓶的形状是
B
.
分析:本题为注水入杯的问题,其实是以水面上升的速度来考察函数的定义,考察因变量与自变量之间的关系,此题关键是依据水杯的形状来决定水面的高度上升的速率的变化,以此来找出相关的函数图象.
解答:解:a中的图象是直线上升的,故其对应的水杯应是柱体,故应填C;
b中的图象上升的速率越来越快,其对应的水杯形状应是下粗上细形状,故应填B;
c的图象上升的速度先变慢再变快,故其对应的水杯形状应是由下往上先由细变粗再由粗变细形状,故应填D;
d中的图象上升的速率变化是越来越慢,故其对应的水杯形状应是下细上粗型,故应选A;
故应依次填 (1)C,(2)A,(3)D,(4)B.
b中的图象上升的速率越来越快,其对应的水杯形状应是下粗上细形状,故应填B;
c的图象上升的速度先变慢再变快,故其对应的水杯形状应是由下往上先由细变粗再由粗变细形状,故应填D;
d中的图象上升的速率变化是越来越慢,故其对应的水杯形状应是下细上粗型,故应选A;
故应依次填 (1)C,(2)A,(3)D,(4)B.
点评:本题考查函数的定义与图象,这是近几年对函数性质考查的一个新题型,值得关注.

练习册系列答案
相关题目
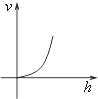 如图所示,向高为H的水瓶A,B,C,D,同时以等速注水,注满为止;若水量v与水深h的图象是如图中的b,则水瓶的形状是( )
如图所示,向高为H的水瓶A,B,C,D,同时以等速注水,注满为止;若水量v与水深h的图象是如图中的b,则水瓶的形状是( )