题目内容
已知函数 .
.
(1)解不等式 ;
;
(2)若 ,且
,且 ,求证:
,求证: .
.
 .
.(1)解不等式
 ;
;(2)若
 ,且
,且 ,求证:
,求证: .
.(1)不等式 的解集为
的解集为 ;(2)证明过程详见解析.
;(2)证明过程详见解析.
 的解集为
的解集为 ;(2)证明过程详见解析.
;(2)证明过程详见解析.试题分析:本题考查解绝对值不等式和证明不等式,意在考查考生运用函数零点分类讨论的解题思想.第一问,利用函数零点将绝对值去掉,将函数转化为分段函数,分类讨论解不等式;第二问,先利用已知函数将所证结论进行转化变成
 ,再利用作差法先证
,再利用作差法先证 ,再开方即可.
,再开方即可.试题解析:(Ⅰ)
 ,
,当
 时,由
时,由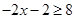 ,解得
,解得 ;
;当
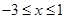 时,
时, 不成立;
不成立;当
 时,由
时,由 ,解得
,解得 . …4分
. …4分所以不等式
 的解集为
的解集为 . …5分
. …5分(Ⅱ)
 即
即 . …6分
. …6分因为
 ,
,所以
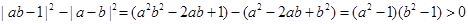 ,
,所以
 .
.故所证不等式成立. …10分

练习册系列答案
相关题目
 +abc≥2
+abc≥2 .
. ,
, .
. 的最小值;
的最小值; .
. ,
,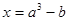 ,
, ,试比较
,试比较 与
与 的大小.
的大小. 且
且 ,则下列不等式中成立的是( )
,则下列不等式中成立的是( )



 ,且
,且 ,则( )
,则( )



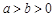 ,则下列不等式一定不成立的是( )
,则下列不等式一定不成立的是( )



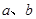 是任意实数,
是任意实数,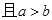 ,则下列不等式成立的是( )
,则下列不等式成立的是( )



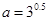 ,
, ,
, ,则 ( )
,则 ( )


