题目内容
若2sinx=1+cosx,则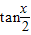 的值等于( )
的值等于( )A.

B.
 或不存在
或不存在C.2
D.2或

【答案】分析:将x看成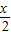 的二倍,利用倍角公式将已知等式的两边展开,化简整理得cos
的二倍,利用倍角公式将已知等式的两边展开,化简整理得cos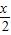 =0或2sin
=0或2sin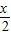 =cos
=cos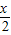 ,再结合同角三角函数的基本关系,即可算出
,再结合同角三角函数的基本关系,即可算出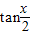 的值.
的值.
解答:解:∵2sinx=1+cosx,
∴2×2sin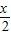 cos
cos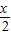 =1+(2cos2
=1+(2cos2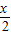 -1),
-1),
即4sin cos
cos =2cos2
=2cos2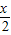 ,可得cos
,可得cos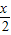 (2sin
(2sin -cos
-cos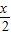 )=0
)=0
因此,cos =0或2sin
=0或2sin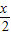 =cos
=cos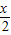
∵ =
=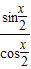 ,∴
,∴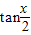 =
= 或
或 不存在
不存在
故选:B
点评:本题给出关于x的三角函数方程,求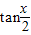 的值,着重考查了二倍角的三角公式和同角三角函数的基本关系等知识,属于基础题.
的值,着重考查了二倍角的三角公式和同角三角函数的基本关系等知识,属于基础题.
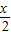 的二倍,利用倍角公式将已知等式的两边展开,化简整理得cos
的二倍,利用倍角公式将已知等式的两边展开,化简整理得cos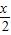 =0或2sin
=0或2sin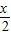 =cos
=cos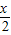 ,再结合同角三角函数的基本关系,即可算出
,再结合同角三角函数的基本关系,即可算出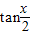 的值.
的值.解答:解:∵2sinx=1+cosx,
∴2×2sin
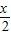 cos
cos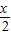 =1+(2cos2
=1+(2cos2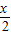 -1),
-1),即4sin
 cos
cos =2cos2
=2cos2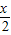 ,可得cos
,可得cos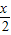 (2sin
(2sin -cos
-cos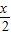 )=0
)=0因此,cos
 =0或2sin
=0或2sin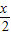 =cos
=cos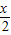
∵
 =
=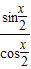 ,∴
,∴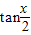 =
= 或
或 不存在
不存在故选:B
点评:本题给出关于x的三角函数方程,求
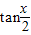 的值,着重考查了二倍角的三角公式和同角三角函数的基本关系等知识,属于基础题.
的值,着重考查了二倍角的三角公式和同角三角函数的基本关系等知识,属于基础题. 
练习册系列答案
相关题目
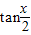 的值等于( )
的值等于( )
 或不存在
或不存在
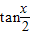 的值等于( )
的值等于( )
 或不存在
或不存在