Question

选修4-5：不等式选讲
已知f（x）=|x-2|．
（I）解不等式：xf（x）+3＞0；
（II）对任意x∈（-3，3），不等式f（x）＜m-|x|成立，求m的取值范围．

Answer 1

分析：（I）由f（x）=|x-2|，知xf（x）+3＞0，x|x-2|+3＞0，由此进行分类讨论，能求出xf（x）+3＞0的解集．
（II）由不等式f（x）＜m-|x|，知y=|x-2|+|x|=

-(x-2)-x，x≤0 -(x-2)+x，0＜x≤2 (x-2)+x，x＞2

，作出函数y=|x-2|+|x|的图象，能推导出对任意x∈（-3，3），不等式f（x）＜m-|x|成立时，m的取值范围．

解答：解：（I）∵f（x）=|x-2|，xf（x）+3＞0，
∴x|x-2|+3＞0，
当x≥2时，不等式为x²-2x+3＞0，
即（x-1）²+2＞0，
此不等式恒成立，故x≥2．
当x＜2时，不等式为-x²+2x+3＞0，解得-1＜x＜3，
故-1＜x＜2．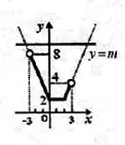
∴不等式：xf（x）+3＞0的解集为{x|x＞-1}．
（II）不等式f（x）＜m-|x|为|x-2|+|x|＜m，
∵y=|x-2|+|x|=

-(x-2)-x，x≤0 -(x-2)+x，0＜x≤2 (x-2)+x，x＞2

，
∴y=

-2x+2，x≤0 2，0＜x≤2 2x-2，x＞2

．
作出函数y=|x-2|+|x|的图象如图：
当-3＜x＜3时，2≤|x-2|+|x|＜8，
∴对任意x∈（-3，3），不等式f（x）＜m-|x|成立时，m的取值范围是{m|m≥8}．

点评：本题考查不等式的解法和满足条件的实数的取值范围的求法，解题时要认真审题，注意分类讨论思想、等价转化思想、数形结合思想的合理运用．