题目内容
14.已知直线l1:ax+3y-1=0与直线l2:2x+(a-1)y+1=0平行,则实数a为( )| A. | 3 | B. | -2 | C. | 3或-2 | D. | 以上都不对 |
分析 对a分类讨论,再把直线的方程化为斜截式,利用两条直线平行的充要条件即可得出
解答 解:当a=0或1时,l1与l2不平行;
当a≠0或1时,直线l1:l1:ax+3y-1=0与直线l2:2x+(a-1)y+1=0,
分别化为:y=-$\frac{1}{3}$ax+$\frac{1}{3}$,y=$\frac{2}{1-a}$x+$\frac{1}{1-a}$,
∵l1∥l2,∴-$\frac{1}{3}$a=$\frac{2}{1-a}$,且$\frac{1}{3}$≠$\frac{1}{1-a}$,
解得a=3或-2.
而a=-2时不满足题意,舍去.
∴a=3.
故选:A.
点评 本题考查了分类讨论、斜截式、两条直线平行的充要条件,考查了推理能力,属于基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知a=log32,b=log30.5,c=1.10.5,那么a、b、c的大小关系为( )
| A. | b>c>a | B. | b>a>c | C. | a>b>c | D. | c>a>b |
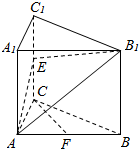 已知直棱柱ABC-A1B1C1,∠ACB=60°,AC=BC=4,AA1=6,E、F分别是棱CC1、AB的中点.
已知直棱柱ABC-A1B1C1,∠ACB=60°,AC=BC=4,AA1=6,E、F分别是棱CC1、AB的中点.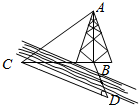 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在C测得塔顶A的仰角为60°,则塔的高度为15$\sqrt{6}$m.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在C测得塔顶A的仰角为60°,则塔的高度为15$\sqrt{6}$m.