题目内容
抛物线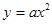 的准线方程是
的准线方程是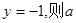 的值为 。
的值为 。
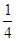
解析试题分析:∵抛物线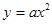 可化为
可化为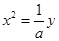 ,∴
,∴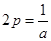 即
即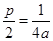 ,由题意
,由题意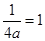 ,故a=
,故a=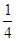
考点:本题考查了抛物线方程的性质
点评:对于此类问题首先把抛物线化为标准方程,然后利用抛物线的性质求解即可

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
抛物线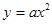 的准线方程是
的准线方程是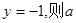 的值为 。
的值为 。
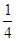
解析试题分析:∵抛物线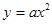 可化为
可化为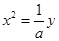 ,∴
,∴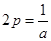 即
即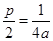 ,由题意
,由题意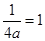 ,故a=
,故a=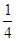
考点:本题考查了抛物线方程的性质
点评:对于此类问题首先把抛物线化为标准方程,然后利用抛物线的性质求解即可

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案