题目内容
某几何体的三视图如图所示,则该几何体的体积不可能是( )
A. | B. | C. | D. |
D
解析试题分析:观察三视图可知,这是一个三棱锥,底面直角三角形一直角边长为2,设另一边长为x,则几何体高为 ,所以几何体体积为,
,所以几何体体积为, <3,故选D。
<3,故选D。
考点:本题主要考查三视图,几何体的体积计算,均值定理的应用。
点评:中档题,三视图是高考必考题目,因此,要明确三视图视图规则,准确地还原几何体,明确几何体的特征,以便进一步解题。三视图视图过程中,要注意虚线的出现,意味着有被遮掩的棱。

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
正方体的体积是64,则其表面积是( )
| A.64 | B.16 | C.96 | D.无法确定 |
如图是一个几何体的三视图,则该几何体为
| A.球 | B.圆柱 |
| C.圆台 | D.圆锥 |
将一个等腰梯形绕着它的较长的底边所在的直线旋转一周,所得的几何体包括
| A.一个圆台、两个圆锥 | B.两个圆台、一个圆柱 |
| C.两个圆台、一个圆锥 | D.一个圆柱、两个圆锥 |
几何体的三视图如图,则几何体的体积为
A. | B. | C. | D. |
半径为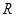 的半圆卷成一个圆锥,则它的体积为( ).
的半圆卷成一个圆锥,则它的体积为( ).
A.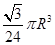 | B. | C. | D. |
从一个正方体中截去部分几何体,得到的几何体三视图如下,则此几何体的体积是( )
| A.64 | B. | C. | D. |
 的底面边长为
的底面边长为 ,高
,高 ,点
,点 在高
在高 上,且
上,且 ,记过点
,记过点 的球的半径为
的球的半径为 ,则函数
,则函数




 的棱长为1,动点P在此正方体的表面上运动,且
的棱长为1,动点P在此正方体的表面上运动,且 ,记点P的轨迹的长度为
,记点P的轨迹的长度为 ,则函数的图像
,则函数的图像
