题目内容
【题目】在平面四边形
中，已知
的面积是
的面积的3倍，若存在正实数
使得
成立,则
的最小值为（ ）
A.
B.
C.
D.
【答案】D
【解析】
由△ACB面积是△ADC面积的3倍，结合三角形的面积公式可知3DF＝BE，然后结合相似三角形的性质可转化为3
，然后结合向量加减法的三角形法则可用
，
表示
，然后根据向量共线定理可设
，结合已知可求
＝10，然后由
，利用基本不等式可求
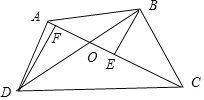
根据题意，如图，连接AC、BD，设AC与BD交于点O，过点B作BE⊥AC与点E，过点D作DF⊥AC与点F，
若△ACB面积是△ADC面积的3倍，即3DF＝BE，
根据相似三角形的性质可知，3，
∴3（
）＝
，
∴
，
设＝
，
∵
＝
，
∴
∴＝10，
∴
当且仅当
且＝10，即x＝
时取等号
故答案为：
．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
