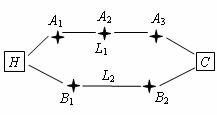
题目内容
(本题满分11分)在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,C=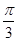 .
.
(1)若△ABC的面积等于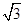 ,求a,b;
,求a,b;
(2)若sinC+sin(B-A)=2sin2A,求△ABC的面积.
(1)a=2,b=2.(2)S= absinC=
absinC= .
.
【解析】
试题分析:(1)由余弦定理及已知条件得,a2+b2-ab=4,…………2分
又因为△ABC的面积等于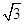 ,所以
,所以 absinC=
absinC=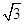 ,得ab=4.…………4分
,得ab=4.…………4分
联立方程组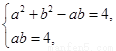 解得a=2,b=2.…………5分
解得a=2,b=2.…………5分
(2)由题意得sin(B+A)+sin(B-A)=4sinAcosA,即sinBcosA=2sinAcosA,…………7分
当cosA=0时,A=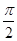 ,B=
,B= ,a=
,a=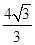 ,b=
,b= ,…………8分
,…………8分
当cosA≠0时,得sinB=2sinA,由正弦定理得b=2a,联立方程组
解得a= ,b=
,b=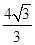 .…………10分
.…………10分
所以△ABC的面积S= absinC=
absinC= .…………11分
.…………11分
考点:本题主要考查正弦定理、余弦定理的应用,三角形内角和定理,两角和差的三角函数。
点评:典型题,本题在考查正弦定理、余弦定理的应用,三角形内角和定理,两角和差的三角函数的同时,考查了函数方程思想,在两道小题中,均通过建立方程组,以便求的a,b,c等。

(本题满分14分)
有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
|
|
优秀 |
非优秀 |
总计 |
|
甲班 |
10 |
|
|
|
乙班 |
|
30 |
|
|
合计 |
|
|
105 |
已知在全部105人中抽到随机抽取1人为优秀的概率为
(1)请完成上面的列联表;
(2)根据列联表的数据,若按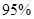 的可靠性要求,能否认为“成绩与班级有关系” .
的可靠性要求,能否认为“成绩与班级有关系” .
(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.