题目内容
已知f(x)定义在R上的函数,对于任意的实数a,b都有f(ab)=af(b)+bf(a),且f(2)=1.(1)求f(
 )的值
)的值(2)求f(2-n)的解析式(n∈N*)
【答案】分析:(1)先对a,b赋值1求出f(1),在利用f(1)=f(2× )即可求出f(
)即可求出f( )的值;
)的值;
(2)先利用条件找到2nf(2-n)=2n-1f(21-n)-2-1.再利用结论构造出一个等差数列,求出等差数列的通项进而求出f(2-n)的解析式.
解答:解:(1)令a=b=1求得f(1)=0(2分)
又f(1)=f(2× )=2f(
)=2f( )+
)+ f(2)∴f(
f(2)∴f( )=-
)=- (5分)
(5分)
(2)f(2-n)=f(2-1•21-n)=2-1f(21-n)+21-nf(2-1),
∴2nf(2-n)=2n-1f(21-n)-2-1.
令bn=2nf(2-n),∴bn=bn-1-2-1,(9分)
∴数列{bn}是以公差d=- b1=2f(
b1=2f( )=-
)=- 的等差数列(12分)
的等差数列(12分)
∴bn=b1+(n-1)•(- ),∴bn=-
),∴bn=-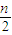 ,∴f(2-n)=-
,∴f(2-n)=- (14分)
(14分)
点评:一般情况下,当具体的函数解析式没有却要找具体的函数值时,其常用方法是用赋值法.
 )即可求出f(
)即可求出f( )的值;
)的值;(2)先利用条件找到2nf(2-n)=2n-1f(21-n)-2-1.再利用结论构造出一个等差数列,求出等差数列的通项进而求出f(2-n)的解析式.
解答:解:(1)令a=b=1求得f(1)=0(2分)
又f(1)=f(2×
 )=2f(
)=2f( )+
)+ f(2)∴f(
f(2)∴f( )=-
)=- (5分)
(5分)(2)f(2-n)=f(2-1•21-n)=2-1f(21-n)+21-nf(2-1),
∴2nf(2-n)=2n-1f(21-n)-2-1.
令bn=2nf(2-n),∴bn=bn-1-2-1,(9分)
∴数列{bn}是以公差d=-
 b1=2f(
b1=2f( )=-
)=- 的等差数列(12分)
的等差数列(12分)∴bn=b1+(n-1)•(-
 ),∴bn=-
),∴bn=-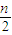 ,∴f(2-n)=-
,∴f(2-n)=- (14分)
(14分)点评:一般情况下,当具体的函数解析式没有却要找具体的函数值时,其常用方法是用赋值法.

练习册系列答案
相关题目