题目内容
(本题12分)设函数 在
在 内有极值。
内有极值。
(1)求实数 的取值范围;
的取值范围;
(2)若 分别为
分别为 的极大值和极小值,记
的极大值和极小值,记 ,求S的取值范围。
,求S的取值范围。
(注: 为自然对数的底数)
为自然对数的底数)
【答案】
(1) ; (2)
; (2) 。
。
【解析】本试题主要是考查了运用导数研究函数的极值的运用。
(1)先求解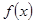 的定义域为
的定义域为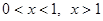
然后求解导数
由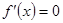 在
在 内有解,得到结论。
内有解,得到结论。
(2)由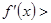 0得
0得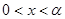 或
或 ,
,
由 得
得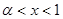 或
或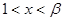
所以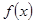 在
在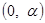 内递增,在
内递增,在 内递减,
内递减,
在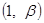 内递减,在
内递减,在 内递增
内递增
得到m,n与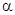 ,
, 的关系,进而结合函数单调性得到结论。
的关系,进而结合函数单调性得到结论。
解: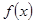 的定义域为
的定义域为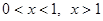 (1分)
(1分)
(1) (2分)
(2分)
由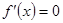 在
在 内有解,
内有解,
令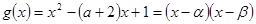 ,
,
不妨设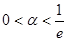 ,则
,则 (3分)
(3分)
所以 ,(4分)
,(4分)
解得: (5分)
(5分)
(2)由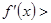 0得
0得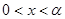 或
或 ,
,
由 得
得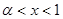 或
或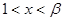
所以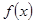 在
在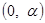 内递增,在
内递增,在 内递减,
内递减,
在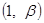 内递减,在
内递减,在 内递增,(7分)
内递增,(7分)
所以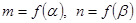
因为 ,
,
所以
 (9分)
(9分)
记 ,
,
所以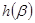 在
在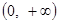 单调递减,所以
单调递减,所以 (11分)
(11分)
又当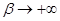 时,
时,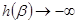
所以 (12分)
(12分)

练习册系列答案
相关题目
 ,
, 时,
时, 取得极值,求
取得极值,求 的值,并求出
的值,并求出 的最小值
的最小值 的表达式.
的表达式. ,曲线
,曲线 在点M
在点M 处的切线方程为
处的切线方程为 .
. 的解析式; (2)求函数
的解析式; (2)求函数 和直线
和直线 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值. ,曲线
,曲线 在点M
在点M 处的切线方程为
处的切线方程为 .
. 的解析式; (2)求函数
的解析式; (2)求函数 和直线
和直线 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.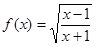 的定义域为A, 函数
的定义域为A, 函数 (其中
(其中 )的定义域为B.
)的定义域为B.  ,当a=0时,求
,当a=0时,求 ;
; , 求实数
, 求实数 的取值范围.
的取值范围.