题目内容
已知 上是增函数,那么实数a的取值范围是
上是增函数,那么实数a的取值范围是
( )
A.(1,+ ) ) | B.( ) ) | C. | D.(1,3) |
C
解析试题分析:因为根据题意可知,要使得函数在R上递增,则满足 对数函数a>1,同时依次函数3-a>0,1<a<3,同时当x=1时,满足3-a-a loga1=0,
loga1=0, ,故答案为
,故答案为 ,选C.
,选C.
考点:本题主要考查了分段函数的单调性问题的运用。
点评:解决该试题的关键是理解分段函数在R上递增,则满足每一段函数都是递增的,而一个易丢的条件就是在断点处的函数值,左侧在该点的函数值要小于等于右侧的在该点函数的函数值。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
函数 的增区间是( )
的增区间是( )
A.( ,2] ,2] | B.[2,  ) ) | C.( ,3] ,3] | D.[3,  ) ) |
已知函数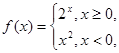 则
则 ( )
( )
| A.16 | B. | C.4 | D.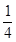 |
当 时,幂函数
时,幂函数 为减函数,则实数
为减函数,则实数 ( )
( )
| A.m=2 | B.m= 1 1 | C.m=2或m=1 | D. |
函数 与
与 的图象( )
的图象( )
| A.关于原点对称 | B.关于 轴对称 轴对称 |
C.关于 轴对称. 轴对称. | D.关于 对称 对称 |
下列函数中,在(0,2)上为增函数的是( )
A.y=log (x+1) (x+1) | B.y=log2 |
C.y=log2 | D.y=log (x2-4x+5) (x2-4x+5) |
已知函数 ,则
,则 等于( )
等于( )
| A.4 | B. | C. | D. |
已知 ,
, ,
, ,则
,则 的大小关系是
的大小关系是
A. | B. |
C.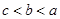 | D. |
 、
、 、
、 、
、 在同一坐标系中的图象如图所示,则
在同一坐标系中的图象如图所示,则 与1的大小关系为 ( )
与1的大小关系为 ( )



