题目内容
9.根据正弦函数、余弦函数的图象,写出使下列不等式成立的x的取值集合:(1)sinx≥$\frac{\sqrt{3}}{2}$(x∈R);
(2)$\sqrt{2}$+2cosx≥0(x∈R).
分析 (1)由sinx≥$\frac{\sqrt{3}}{2}$(x∈R),结合正弦函数的图象可得x的范围.
(2)由$\sqrt{2}$+2cosx≥0(x∈R),可得cosx≥-$\frac{\sqrt{2}}{2}$,结合余弦函数的图象可得x的范围.
解答 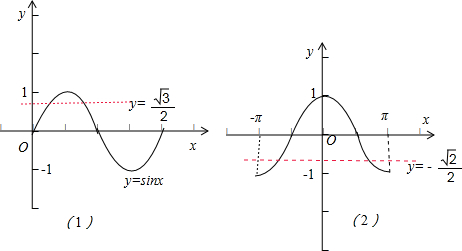 解:(1)由sinx≥$\frac{\sqrt{3}}{2}$(x∈R),结合正弦函数在一个周期上的图象,
解:(1)由sinx≥$\frac{\sqrt{3}}{2}$(x∈R),结合正弦函数在一个周期上的图象,
如图(1)所示,
可得x的范围为{x|2kπ+$\frac{π}{3}$≤x≤2kπ+$\frac{2π}{3}$,k∈z}.
(2)由$\sqrt{2}$+2cosx≥0(x∈R),可得cosx≥-$\frac{\sqrt{2}}{2}$,
结合余弦函数在一个周期上的图象如图(2)所示,
可得x的范围为{x|2kπ-$\frac{3π}{4}$≤x≤2kπ+$\frac{3π}{4}$,k∈z}.
点评 本题主要考查正弦函数的图象、余弦函数的图象,属于基础题.

练习册系列答案
相关题目
19.独立性检验中,假设H0:变量X与变量Y没有关系.则在H0成立的情况下,估算概率p(k2≥10.83)≈0.001表示的意义是( )
| A. | 变量X与变量Y有关系的概率为0.1% | |
| B. | 变量X与变量Y有关系的概率为99% | |
| C. | 变量X与变量Y没有关系的概率为99% | |
| D. | 变量X与变量Y有关系的概率为99.9% |
14.经过点(m,3)和(2,m)的直线l与斜率为-4的直线互相垂直,则m的值是( )
| A. | 2 | B. | $\frac{14}{5}$ | C. | $\frac{10}{3}$ | D. | 4 |
1.抛物线x2=-4y的焦点为F,若抛物线上存在一点P,使得P到直线y=1的距离与到直线kx-y+2k+2=0的距离之和的最小值达到最大,则k的值为( )
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
18.已知函数y=sin2x+cosx+$\frac{3}{4}(x∈[0,\frac{2π}{3}])$,则函数的值域为( )
| A. | $[-\frac{1}{4},\frac{7}{4}]$ | B. | [1,2] | C. | $[-\frac{3}{4},1]$ | D. | $[-\frac{1}{4},2]$ |
