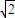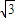题目内容
设双曲线x2-my2=1离心率不小于
,此双曲线焦点到渐近线的最小距离为( )
| 3 |
分析:将双曲线化成标准形式,可以求出a=1,b=
,c=
.利用离心率e不小于
建立不等式,解之可得
≥2,最后利用点到直线距离的公式求出d=
,从而得到双曲线焦点到渐近线的最小距离为
.
| 1 | ||
|
1+
|
| 3 |
| 1 |
| m |
|
| 2 |
解答:解:将双曲线x2-my2=1化为标准形式,可得x2-
=1,说明m>0,
∴a=1,b=
可得c=
=
,
∴双曲线焦点为(±
,0),
∵离心率e≥
,
∴
=
≥
⇒
≥2,
又∵双曲线渐近线为x±
y=0,
∴此双曲线焦点到渐近线的距离为d=
=
≥
,
故选A
| y2 | ||
|
∴a=1,b=
| 1 | ||
|
| a2+b2 |
1+
|
∴双曲线焦点为(±
1+
|
∵离心率e≥
| 3 |
∴
| c |
| a |
1+
|
| 3 |
| 1 |
| m |
又∵双曲线渐近线为x±
| m |
∴此双曲线焦点到渐近线的距离为d=
|
| ||||
|
|
| 2 |
故选A
点评:本题以含有字母参数的双曲线求焦点到渐近线的最小距离为例,着重考查了双曲线的基本概念和一些简单性质,考查了点到直线距离公式和不等式的解法,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 ,此双曲线焦点到渐近线的最小距离为
,此双曲线焦点到渐近线的最小距离为

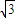 ,此双曲线焦点到渐近线的最小距离为( )
,此双曲线焦点到渐近线的最小距离为( )