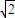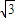题目内容
设双曲线x2-my2=1离心率不小于 ,此双曲线焦点到渐近线的最小距离为
,此双曲线焦点到渐近线的最小距离为
- A.

- B.

- C.

- D.2
A
分析:将双曲线化成标准形式,可以求出a=1,b=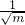 ,c=
,c=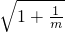 .利用离心率e不小于
.利用离心率e不小于 建立不等式,解之可得
建立不等式,解之可得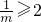 ,最后利用点到直线距离的公式求出d=
,最后利用点到直线距离的公式求出d= ,从而得到双曲线焦点到渐近线的最小距离为
,从而得到双曲线焦点到渐近线的最小距离为 .
.
解答:将双曲线x2-my2=1化为标准形式,可得 ,说明m>0,
,说明m>0,
∴a=1,b=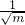 可得
可得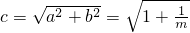 ,
,
∴双曲线焦点为(±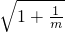 ,0),
,0),
∵离心率e≥ ,
,
∴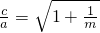 ≥
≥ ?
?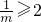 ,
,
又∵双曲线渐近线为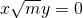 ,
,
∴此双曲线焦点到渐近线的距离为d=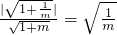 ≥
≥ ,
,
故选A
点评:本题以含有字母参数的双曲线求焦点到渐近线的最小距离为例,着重考查了双曲线的基本概念和一些简单性质,考查了点到直线距离公式和不等式的解法,属于中档题.
分析:将双曲线化成标准形式,可以求出a=1,b=
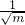 ,c=
,c=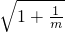 .利用离心率e不小于
.利用离心率e不小于 建立不等式,解之可得
建立不等式,解之可得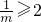 ,最后利用点到直线距离的公式求出d=
,最后利用点到直线距离的公式求出d= ,从而得到双曲线焦点到渐近线的最小距离为
,从而得到双曲线焦点到渐近线的最小距离为 .
.解答:将双曲线x2-my2=1化为标准形式,可得
 ,说明m>0,
,说明m>0,∴a=1,b=
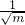 可得
可得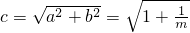 ,
,∴双曲线焦点为(±
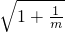 ,0),
,0),∵离心率e≥
 ,
,∴
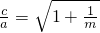 ≥
≥ ?
?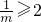 ,
,又∵双曲线渐近线为
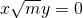 ,
,∴此双曲线焦点到渐近线的距离为d=
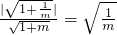 ≥
≥ ,
,故选A
点评:本题以含有字母参数的双曲线求焦点到渐近线的最小距离为例,着重考查了双曲线的基本概念和一些简单性质,考查了点到直线距离公式和不等式的解法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
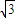 ,此双曲线焦点到渐近线的最小距离为( )
,此双曲线焦点到渐近线的最小距离为( )