题目内容
在平面直角坐标系中,若点 在直线
在直线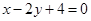 的右下方区域包括边界,则
的右下方区域包括边界,则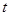 的取值范围是( )
的取值范围是( )
A. | B.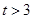 | C.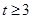 | D.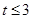 |
D
解析试题分析:先作图可知,当点点 在直线
在直线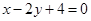 的右下方区域包括边界,那么可知包括(0,0)点,而将(0,0)代入可知4
的右下方区域包括边界,那么可知包括(0,0)点,而将(0,0)代入可知4 0,因此可知在其右下方包括边界的所有点代入之后都满足
0,因此可知在其右下方包括边界的所有点代入之后都满足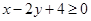 ,故
,故 代入得到,2-2t+4
代入得到,2-2t+4 0,得到3
0,得到3 t,故选D.
t,故选D.
考点:本试题主要考查了二元一次不等式表示的平面区域的问题的运用。
点评:解决该试题的关键是先判定其右下方的区域满足的不等式的符号是 还是
还是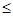 即可。
即可。

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
若 满足约束条件
满足约束条件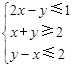 ,目标函数
,目标函数 仅在点
仅在点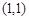 处取得小值,则k的取值范围为
处取得小值,则k的取值范围为
| A.(-1,2) | B.(-4,2) | C.(-4,0] | D.(-2,4) |
设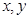 满足约束条件
满足约束条件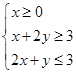 ,则
,则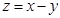 的最大值是( )
的最大值是( )
A. | B.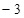 | C.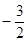 | D.0 |
已知实数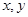 满足条件
满足条件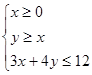 ,则
,则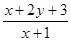 的最大值是( )
的最大值是( )
A.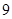 | B.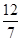 | C.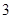 | D.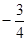 |
已知实数对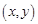 满足不等式组
满足不等式组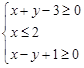 ,二元函数
,二元函数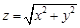 的最大值为( )
的最大值为( )
A.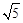 | B.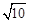 | C.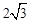 | D.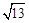 |
已知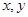 满足条件
满足条件 则
则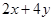 的最小值为( )
的最小值为( )
| A.6 | B.12 | C.-6 | D.-12 |
若实数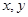 满足不等式组
满足不等式组 (
( 为常数),且
为常数),且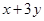 的最大值为12,
的最大值为12,
则实数 =( )
=( )
| A.0 | B. | C.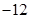 | D.任意实数 |
电视台应某企业之约播放两套连续剧.其中,连续剧甲每次播放时间为80 min,其中广告时间为1 min,收视观众为60万;连续剧乙每次播放时间为40 min,其中广告时间为1 min,收视观众为20万.已知该企业与电视台达成协议,要求电视台每周至少播放6 min广告,而电视台每周只能为该企业提供不多于320 min的节目时间.则该电视台通过这两套连续剧所获得的收视观众最多为
| A.220万 | B.200万 | C.180万 | D.160万 |
已知变量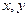 满足
满足 则
则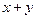 的最大值是( )
的最大值是( )
| A.6 | B.5 | C.4 | D.3 |