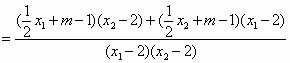Question

已知椭圆的中心在原点， 焦点在x轴上，长轴长是短轴长的2倍，且经过点M(2，1)，平行于OM直线l在y轴上的截距为m(m＜0)，设直线l交椭圆于两个不同点A、B．

(1)求椭圆方程；

(2)求证：对任意的m的允许值，△ABM的内心I在定直线x＝2上．

Answer 1

答案：
解析：

解：(1)设椭圆方程为 　　则 　　所以，椭圆方程为 　　(2)如图，因为直线平行于OM，且在轴上的截距为，又，所以，直线的方程为，由， 　　设，则， 　　设直线MA、MB的斜率分别为、，则， 　　故 　　 　　＝ 　　 　　故＝0，所以，的角平分线MI垂直x轴，因此，内心I的横坐标等于点M的横坐标，则对任意的，的内心I在定直线．