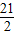题目内容
若椭圆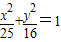 和双曲线
和双曲线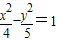 的共同焦点为F1,F2,P是两曲线的一个交点,则|PF1|•|PF2|的值为( )
的共同焦点为F1,F2,P是两曲线的一个交点,则|PF1|•|PF2|的值为( )A.
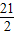
B.84
C.3
D.21
【答案】分析:设|PF1|>|PF2|,根据椭圆和双曲线的定义可分别表示出|PF1|+|PF2|和|PF1|-|PF2|,进而可表示出|PF1|和|PF2|,根据焦点相同进而可求得|pF1|•|pF2|的表达式.
解答:解:由椭圆和双曲线定义
不妨设|PF1|>|PF2|
则|PF1|+|PF2|=10
|PF1|-|PF2|=4
所以|PF1|=7
|PF2|=3
∴|pF1|•|pF2|=21
故选D.
点评:本题主要考查了圆锥曲线的共同特征,解答关键是正确运用椭圆和双曲线的简单的几何性质.
解答:解:由椭圆和双曲线定义
不妨设|PF1|>|PF2|
则|PF1|+|PF2|=10
|PF1|-|PF2|=4
所以|PF1|=7
|PF2|=3
∴|pF1|•|pF2|=21
故选D.
点评:本题主要考查了圆锥曲线的共同特征,解答关键是正确运用椭圆和双曲线的简单的几何性质.

练习册系列答案
相关题目
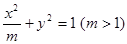 和双曲线
和双曲线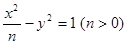 有共同的焦点F1、F2,且P是两条曲线的一个交点,则△PF1F2的面积是( )
有共同的焦点F1、F2,且P是两条曲线的一个交点,则△PF1F2的面积是( )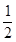 C.2
D.4
C.2
D.4 和双曲线
和双曲线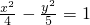 的共同焦点为F1,F2,P是两曲线的一个交点,则|PF1|•|PF2|的值为
的共同焦点为F1,F2,P是两曲线的一个交点,则|PF1|•|PF2|的值为
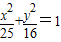 和双曲线
和双曲线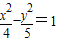 的共同焦点为F1,F2,P是两曲线的一个交点,则|PF1|•|PF2|的值为( )
的共同焦点为F1,F2,P是两曲线的一个交点,则|PF1|•|PF2|的值为( )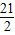
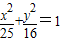 和双曲线
和双曲线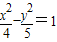 的共同焦点为F1,F2,P是两曲线的一个交点,则|PF1|•|PF2|的值为( )
的共同焦点为F1,F2,P是两曲线的一个交点,则|PF1|•|PF2|的值为( )