题目内容
已知椭圆C1与双曲线C2有共同的焦点F1（-2，0），F2（2，0），椭圆的一个短轴端点为B，直线F1B与双曲线的一条渐近线平行，椭圆C1与双曲线C2的离心率分别为e1，e2，则e1+e2取值范围为（ ）
| A．（2，+∞） | B．（4，+∞） | C．（4，+∞） | D．（2，+∞） |
设椭圆的长轴为2a，短轴为2b；双曲线的实轴为2a'，虚轴为2b'
∵椭圆的一个短轴端点为B，直线F1B与双曲线的一条渐近线平行，
∴
=
，平方可得
=
由此得到
=
，即
=
，
也即(
)2=(
)2，可得e1•e2=1
∵e1、e2都是正数，∴e1+e2≥2
=2，且等号不能成立
因此e1+e2取值范围为（2，+∞）
故选：D
∵椭圆的一个短轴端点为B，直线F1B与双曲线的一条渐近线平行，
∴
| b′ |
| a′ |
| b |
| c |
| b′2 |
| a′2 |
| b2 |
| c2 |
由此得到
| a′2+b′2 |
| a′2 |
| c2+b2 |
| c2 |
| c2 |
| a′2 |
| a 2 |
| c2 |
也即(
| c |
| a′ |
| a |
| c |
∵e1、e2都是正数，∴e1+e2≥2
| e1e2 |
因此e1+e2取值范围为（2，+∞）
故选：D
练习册系列答案
相关题目
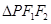是一个以PF1为底的等腰三角形，
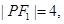C1的离心率为
则C2的离心率