题目内容

（2013•湖南）如图，在半径为
7
的⊙O中，弦AB，CD相交于点P，PA=PB=2，PD=1，则圆心O到弦CD的距离为
3
2
3
2
．
分析：首先利用相交弦定理求出CD的长，再利用勾股定理求出圆心O到弦CD的距离，注意计算的正确率．
解答：解：由相交弦定理得，AP×PB=CP×PD，
∴2×2=CP•1，
解得：CP=4，又PD=1，
∴CD=5，
又⊙O的半径为
7
，
则圆心O到弦CD的距离为d=
r2-(
CD
2
)2
=
7-(
5
2
)2
=
3
2
．
故答案为：
3
2
．
点评：此题主要考查了相交弦定理，垂径定理，勾股定理等知识，题目有一定综合性，是中、高考题的热点问题．
练习册系列答案
相关题目
（2013•湖南）在等腰直角三角形ABC中，AB=AC=4，点P是边AB边上异于AB的一点，光线从点P出发，经BC，CA反射后又回到点P（如图1），若光线QR经过△ABC的重心，则AP等于（　　）
（2013•湖南）某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横直线的交叉点以及三角形顶点）处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收获Y（单位：kg）与它的“相近”作物株数X之间的关系如下表所示：
X 1 2 3 4
Y 51 48 45 42
这里，两株作物“相近”是指它们之间的直线距离不超过1米．
（I）从三角形地块的内部和边界上分别随机选取一株作物，求它们恰 好“相近”的概率；
（II）在所种作物中随机选取一株，求它的年收获量的分布列与数学期望．
（2013•湖南）如图，在直棱柱ABCD-A1B1C1D1中，AD∥BC，∠BAD=90°，AC⊥BD，BC=1，AD=AA1=3．
（Ⅰ）证明：AC⊥B1D；
（Ⅱ）求直线B1C1与平面ACD1所成的角的正弦值．
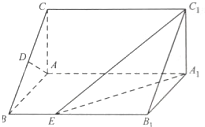（2013•湖南）如图．在直棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=
2
，AA1=3，D是BC的中点，点E在棱BB1上运动．
（1）证明：AD⊥C1E；
（2）当异面直线AC，C1E 所成的角为60°时，求三棱锥C1-A1B1E的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网