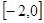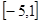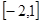题目内容
设函数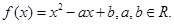
(1)已知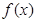 在区间
在区间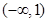 上单调递减,求
上单调递减,求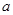 的取值范围;
的取值范围;
(2)存在实数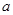 ,使得当
,使得当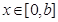 时,
时,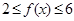 恒成立,求
恒成立,求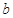 的最大值及此时
的最大值及此时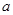 的值.
的值.
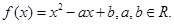
(1)已知
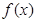 在区间
在区间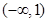 上单调递减,求
上单调递减,求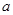 的取值范围;
的取值范围;(2)存在实数
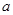 ,使得当
,使得当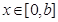 时,
时,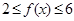 恒成立,求
恒成立,求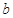 的最大值及此时
的最大值及此时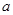 的值.
的值.(1)  (2)
(2) 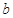 的最大值为3,此时
的最大值为3,此时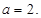
 (2)
(2) 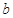 的最大值为3,此时
的最大值为3,此时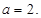
试题分析:
(1)该函数显然是二次函数,开口向上,所以在对称轴左侧单调递减,右侧单调递增.根据题意可知区间
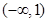 在对称轴的左侧,所以根据对称轴即可求出
在对称轴的左侧,所以根据对称轴即可求出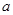 的取值范围;
的取值范围;(2)由于该二次函数的对称轴未知,所以当对称轴与区间处于不同位置时,函数的单调性会发生改变,从而影响到函数的最值,所以得讨论区间与对称轴的位置关系,通过讨论位置关系确定单调性和最值,建立关于
 的关系式,从而得到最终的结论.
的关系式,从而得到最终的结论.试题解析:
(1)该函数显然是二次函数,开口向上,所以在对称轴左侧单调递减,
该函数的对称轴为
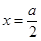 ,所以区间
,所以区间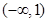 在对称轴
在对称轴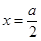 的左侧,
的左侧,即
 所以
所以
(2)显然
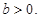
 ,对称轴
,对称轴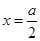
讨论对称轴与区间的位置关系:
(1)当对称轴在区间左侧时,有
 ,即
,即 ,此时函数
,此时函数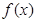 在
在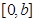 上单调递增,
上单调递增,所以要使
 恒成立,只需满足
恒成立,只需满足
由
 及
及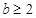 得
得 与
与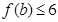 矛盾,舍.
矛盾,舍.(2)当对称轴在区间右侧时,有
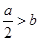 ,此时函数
,此时函数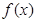 在
在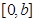 上单调递减,
上单调递减,要使
 恒成立,只需满足
恒成立,只需满足
由
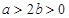 得
得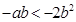 ,
,所以
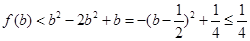 与
与 矛盾,舍.
矛盾,舍.(3)当对称轴在区间内时,有
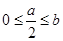 ,此时函数
,此时函数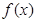 在
在 上递减,在
上递减,在 上递增,
上递增,要使
 恒成立,只需满足
恒成立,只需满足
由前二式得
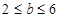 ,由后二式得
,由后二式得
又
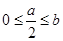 得
得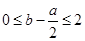 即
即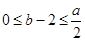 ,故
,故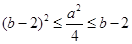
所以
 。当
。当 时,
时,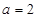 时满足题意.
时满足题意.综上
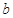 的最大值为3,此时
的最大值为3,此时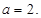

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
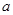 为实数,
为实数, .
.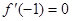 ,求
,求 在
在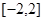 上的最大值和最小值;
上的最大值和最小值;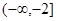 和
和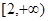 上都是递增的,求
上都是递增的,求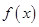 是定义在
是定义在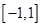 上的奇函数,在
上的奇函数,在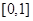 上
上 .
. .
.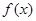 是
是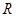 上的奇函数,且当
上的奇函数,且当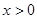 时,
时,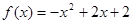 .
.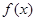 满足
满足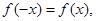 且当
且当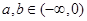 时总有
时总有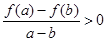 ,其中
,其中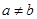 .
. 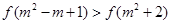 ,则实数
,则实数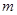 的取值范围是 .
的取值范围是 .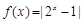 ,当
,当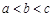 时,有
时,有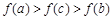 .给出以下结论:
.给出以下结论: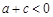 ;(2)
;(2)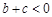 ;(3)
;(3) ;(4)
;(4)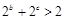 .
.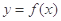 为偶函数,且在区间
为偶函数,且在区间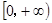 上为增函数,不等式
上为增函数,不等式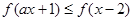 对
对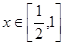 恒成立,则实数
恒成立,则实数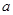 的取值范围为 ( )
的取值范围为 ( )