题目内容
(重庆市2011届高三下学期第二次联合诊断性考试文科)已知函数f(x)=
x3-
x2+x+b
(1)当f(x)=
x3-
x2+x+b时,求函数f(x)=
x3-
x2+x+b的单调区间:
(2)若函数f(x)=
x3-
x2+x+b的图象过点(1,1)且极小值点在区间(1,2)内,求实数b的取值范围.
| a |
| 3 |
| a+1 |
| 2 |
(1)当f(x)=
| a |
| 3 |
| a+1 |
| 2 |
| a |
| 3 |
| a+1 |
| 2 |
(2)若函数f(x)=
| a |
| 3 |
| a+1 |
| 2 |
分析:(1)先求导函数 f′(x),并将导函数分解因式变形为 f′(x)=(x-1)(ax-1),便于解不等式,再确定讨论标准,由于解不等式f′(x)>0和f′(x)<0,需比较a与0,1的大小,故确定分当a>1,当a=1,当0<a<1,当a=0,当a<0五种情况讨论,最后分别在五种情况下解含参数的一元二次不等式即可得函数的单调区间
(2)先由函数f(x)=
x3-
x2+x+b的图象过点(1,1),代入得b=
,再结合(1)中的讨论,若极小值点在区间(1,2)内,需
,从而解得a的范围,最后求一次函数b=
的值域即可得b的范围
(2)先由函数f(x)=
| a |
| 3 |
| a+1 |
| 2 |
| a+3 |
| 6 |
|
| a+3 |
| 6 |
解答:解:(1)∵f′(x)=ax2-(a+1)x+1=(x-1)(ax-1)
当a>1时,0<
<1,由f′(x)>0,得x>1或x<
,由f′(x)<0,得
<x<1,∴函数f(x)的增区间为(-∞,
),(1,+∞);减区间为(
,1)
当a=1时,∵f′(x)=(x-1)2≥0,∴函数f(x)的增区间为(-∞,+∞)
当0<a<1时,
>1,由f′(x)>0,得x<1或x>
,由f′(x)<0,得1<x<
,∴函数f(x)的增区间为(
,+∞),(-∞.1);减区间为(1,
)
当a=0时,f′(x)=(1-x),由f′(x)>0,得x<1,由f′(x)<0,得x>1,∴函数f(x)的增区间为(-∞,1);减区间为(1,+∞)
当a<0时,
<0,由f′(x)>0,得
<x<1,由f′(x)<0,得x>1或x<
,,∴函数f(x)的增区间为(
,1);减区间为(-∞,
),(1,+∞)
综上所述,当a>1时函数f(x)的增区间为(-∞,
),(1,+∞);减区间为(
,1)
当a=1时,函数f(x)的增区间为(-∞,+∞)
当0<a<1时,函数f(x)的增区间为(
,+∞),(-∞.1);减区间为(1,
)
当a=0时,函数f(x)的增区间为(-∞,1);减区间为(1,+∞)
当a<0时,函数f(x)的增区间为(
,1);减区间为(-∞,
),(1,+∞)
(2)∵函数f(x)=
x3-
x2+x+b的图象过点(1,1)
∴1=
-
+1+b,∴b=
∵f(x)极小值点在区间(1,2)内,由(1)可知
∴
<a<1
∴
<
<
∴
<b<
当a>1时,0<
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
当a=1时,∵f′(x)=(x-1)2≥0,∴函数f(x)的增区间为(-∞,+∞)
当0<a<1时,
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
当a=0时,f′(x)=(1-x),由f′(x)>0,得x<1,由f′(x)<0,得x>1,∴函数f(x)的增区间为(-∞,1);减区间为(1,+∞)
当a<0时,
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
综上所述,当a>1时函数f(x)的增区间为(-∞,
| 1 |
| a |
| 1 |
| a |
当a=1时,函数f(x)的增区间为(-∞,+∞)
当0<a<1时,函数f(x)的增区间为(
| 1 |
| a |
| 1 |
| a |
当a=0时,函数f(x)的增区间为(-∞,1);减区间为(1,+∞)
当a<0时,函数f(x)的增区间为(
| 1 |
| a |
| 1 |
| a |
(2)∵函数f(x)=
| a |
| 3 |
| a+1 |
| 2 |
∴1=
| a |
| 3 |
| a+1 |
| 2 |
| a+3 |
| 6 |
∵f(x)极小值点在区间(1,2)内,由(1)可知
|
∴
| 1 |
| 2 |
∴
| 7 |
| 12 |
| a+3 |
| 6 |
| 2 |
| 3 |
∴
| 7 |
| 12 |
| 2 |
| 3 |
点评:本题考察了利用导数求函数的单调区间的方法,导数与函数极值的关系,分类讨论的思想方法,熟练的解含参数的一元二次不等式是解决本题的关键

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
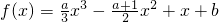
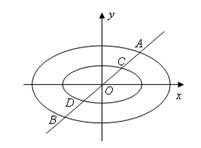 写出与椭圆相似且短半轴长为的椭圆的方程;若在椭圆上存在两点、关于直线对称,求实数的取值范围?
写出与椭圆相似且短半轴长为的椭圆的方程;若在椭圆上存在两点、关于直线对称,求实数的取值范围?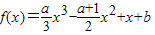
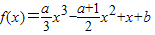 时,求函数
时,求函数 的单调区间:
的单调区间: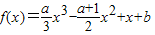 的图象过点(1,1)且极小值点在区间(1,2)内,求实数b的取值范围.
的图象过点(1,1)且极小值点在区间(1,2)内,求实数b的取值范围.