题目内容
过点A(6,0),B(0,4),圆心在l:2x-7y+8=0上的圆的方程为( )
A、(x-3)2+(y-2)2=
| ||
B、(x-2)2+(y-3)2=
| ||
| C、(x-3)2+(y-2)2=13 | ||
| D、(x-2)2+(y-3)2=13 |
分析:设圆的标准方程为(x-a)2+(y-b)2=r2,根据题意建立关于a、b、r的方程组,解之即可得到所求圆的方程.
解答:解:设圆的标准方程为(x-a)2+(y-b)2=r2,
∵点A(6,0)、B(0,4)在圆上,且圆心在l:2x-7y+8=0上,
∴
,解之得
.
由此可得圆的标准方程为(x-3)2+(y-2)2=13.
故选:C
∵点A(6,0)、B(0,4)在圆上,且圆心在l:2x-7y+8=0上,
∴
|
|
由此可得圆的标准方程为(x-3)2+(y-2)2=13.
故选:C
点评:本题给出经过两个定点A、B的圆,已知圆心在定直线上时求圆的标准方程.着重考查了圆的标准方程及其应用的知识,属于基础题.

练习册系列答案
相关题目
 的倾斜角为120°,
的倾斜角为120°, 过点P(1,0)、Q(4,
过点P(1,0)、Q(4, )
)
 ,
,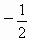 )
)
 )、Q(4,
)、Q(4, )
)
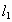 的倾斜角为120°,
的倾斜角为120°, 过点P(1,0)、Q(4,
过点P(1,0)、Q(4, )
) ,
, )
)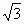 )、Q(4,
)、Q(4, )
)