题目内容
市民李生居住在甲地,工作在乙地,他的小孩就读的小学在丙地,三地之间的道路情
况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机
的.同一条道路去程与回程是否堵车相互独立. 假设李生早上需要先开车送小孩去丙地小学,
再返回经甲地赶去乙地上班.假设道路 、
、 、
、 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是 ,
,
道路 、
、 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.

(1)求李生小孩按时到校的概率;
(2)李生是否有八成把握能够按时上班?
(3)设 表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求
表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求 的均值.
的均值.
况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机
的.同一条道路去程与回程是否堵车相互独立. 假设李生早上需要先开车送小孩去丙地小学,
再返回经甲地赶去乙地上班.假设道路
 、
、 、
、 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是 ,
,道路
 、
、 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.
(1)求李生小孩按时到校的概率;
(2)李生是否有八成把握能够按时上班?
(3)设
 表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求
表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求 的均值.
的均值. (1) (2)李生没有八成把握能够按时上班(3)
(2)李生没有八成把握能够按时上班(3)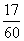
 (2)李生没有八成把握能够按时上班(3)
(2)李生没有八成把握能够按时上班(3)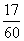
试题分析:⑴因为道路D、E上班时间往返出现拥堵的概率分别是
 和
和 ,
,因此从甲到丙遇到拥堵的概率是

所以李生小孩能够按时到校的概率是
 ;
; ⑵甲到丙没有遇到拥堵的概率是
 ,
, 丙到甲没有遇到拥堵的概率也是
 ,
, 甲到乙遇到拥堵的概率是
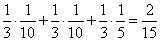 ,
, 甲到乙没有遇到拥堵的概率是
 ,李生上班途中均没有遇到拥堵的概率是
,李生上班途中均没有遇到拥堵的概率是 ,所以李生没有八成把握能够按时上班
,所以李生没有八成把握能够按时上班⑶依题意
 可以取
可以取 .
.  =
= ,
, =
= ,
, =
= ,
, | 0 | 1 | 2 |
 |  |  |  |
 .
.点评:本题着重考查了用树状图列举随机事件出现的所有情况,并求出某些事件的概率,但
应注意在求概率时各种情况出现的可能性务必相同.用到的知识点为:概率=所求情况数与
总情况数之比.

练习册系列答案
相关题目
 ,由于发扬团队精神,此题能解出的概率是 .
,由于发扬团队精神,此题能解出的概率是 . ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是
 ,则这位同学被其中一所学校录取的概率为 ;
,则这位同学被其中一所学校录取的概率为 ;
 ,求向量
,求向量 的概率;
的概率; 构成区域
构成区域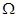 :
: ,求二元数组
,求二元数组
 1的概率.
1的概率. ,则甲回家途中遇红灯次数的期望为( )
,则甲回家途中遇红灯次数的期望为( )



 =
= (
( =1,2,3,4,5).
=1,2,3,4,5). 的值;
的值; ;
;
 ,求随机变量
,求随机变量