题目内容
规定符号“△”表示一种运算,即a△b=| ab |
分析:先根据1△k=
+1+k=3,求得
,进而求得k.把k代入f(x)=k△x得出f(x)=
+x+1,进而可求得函数f(x)的定义域,再利用配方法求得函数f(x)的值域.
| k |
| k |
| x |
解答:解:1△k=
+1+k=3,解得
=1,
∴k=1
∴f(x)=k△x=
+k+x=
+x+1
对于
需x≥0,
∴对于f(x)=
+x+1=(
+
)2+
≥1
故函数f(x)的值域为[1,+∞)
故答案为:[1,+∞)
| k |
| k |
∴k=1
∴f(x)=k△x=
| kx |
| x |
对于
| x |
∴对于f(x)=
| x |
| x |
| 1 |
| 2 |
| 3 |
| 4 |
故函数f(x)的值域为[1,+∞)
故答案为:[1,+∞)
点评:本题主要考查了函数的值域的问题,以及考查阅读题意的能力,属于创新题.

练习册系列答案
相关题目
 ”表示一种两个正实数之间的运算,即a
”表示一种两个正实数之间的运算,即a ,a,b是正实
,a,b是正实 =3,则函数
=3,则函数 的值域是
.
的值域是
. ”表示一种两个正实数之间的运算,即
”表示一种两个正实数之间的运算,即 =
= ,
, 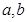 是
是 =3,则函数
=3,则函数 的值域是
的值域是