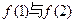题目内容
已知函数f(x)=
x3+
ax2+2bx+c在R上可导.
(1)若f(x)在区间[-1,2]上为减函数,且b=3a,求a的取值范围;
(2)若f(x)的极大值点在(0,1)内,极小值点在(1,2)内,求
的取值范围.
| 1 |
| 3 |
| 1 |
| 2 |
(1)若f(x)在区间[-1,2]上为减函数,且b=3a,求a的取值范围;
(2)若f(x)的极大值点在(0,1)内,极小值点在(1,2)内,求
| b-2 |
| a-1 |
(1)∵当a≠0时,f′(x)=x2+ax+2b=x2+ax+6a,又f(x)在[-1,2]上为减函数,
∴f′(x)≤0对x∈[-1,2]恒成立,…(2分)
即x2+ax+6a≤0对x∈[-1,2]恒成立,
∴f′(-1)≤0且f′(2)≤0,…(4分)
即
⇒
⇒a≤-
.…(6分)
 (2)∵f(x)=
(2)∵f(x)=
x3+
ax2+2bx+c,
∴f′(x)=x2+ax+2b,…(8分)
由题意得
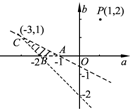
画出可行域:
于是
即为点P(1,2)与可行域内(不包含边界)任意一点的连线的斜率.
∴kPC<
<kPA,即
<
<1.…(13分)
∴f′(x)≤0对x∈[-1,2]恒成立,…(2分)
即x2+ax+6a≤0对x∈[-1,2]恒成立,
∴f′(-1)≤0且f′(2)≤0,…(4分)
即
|
|
| 1 |
| 2 |
 (2)∵f(x)=
(2)∵f(x)=| 1 |
| 3 |
| 1 |
| 2 |
∴f′(x)=x2+ax+2b,…(8分)
由题意得
|
于是
| b-2 |
| a-1 |
∴kPC<
| b-2 |
| a-1 |
| 1 |
| 4 |
| b-2 |
| a-1 |

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 在
在 中的最大值和最小值分别是( )
中的最大值和最小值分别是( )