题目内容
某运动员投篮命中率P=0.6,
(1)求一次投篮时命中次数ξ的期望与方差;
(2)求重复5次投篮时,命中次数η的期望与方差.
解:(1)投篮一次,命中次数ξ的分布列为:
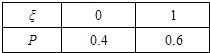
则Eξ=0×0.4+1×0.6=0.6,
Dξ=(0-0.6)2×0.4+(1-0.6)2×0.6=0.24.
(2)由题意,重复5次投篮,命中的次数η服从二项分布,即η~B(5,0.6),
由二项分布期望与方差的结论有:
Eη=np=5×0.6=3,
Dη=np(1-p)=5×0.6×0.4=1.2.
分析:(1)投篮一次有两个结果;命中与不中,因此命中次数ξ服从两点分布;
(2)重复5次投篮可认为是5次独立重复试验,命中次数η服从二项分布.
点评:本题考查了二项分布与n次独立重复试验的模型,离散型随机变量及其分布列,离散型随机变量的期望与方差,属于基础题.
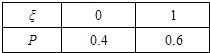
则Eξ=0×0.4+1×0.6=0.6,
Dξ=(0-0.6)2×0.4+(1-0.6)2×0.6=0.24.
(2)由题意,重复5次投篮,命中的次数η服从二项分布,即η~B(5,0.6),
由二项分布期望与方差的结论有:
Eη=np=5×0.6=3,
Dη=np(1-p)=5×0.6×0.4=1.2.
分析:(1)投篮一次有两个结果;命中与不中,因此命中次数ξ服从两点分布;
(2)重复5次投篮可认为是5次独立重复试验,命中次数η服从二项分布.
点评:本题考查了二项分布与n次独立重复试验的模型,离散型随机变量及其分布列,离散型随机变量的期望与方差,属于基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目