题目内容
已知函数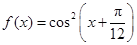 ,
,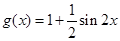 .
.
(1)设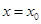 是函数
是函数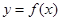 图象的一条对称轴,求
图象的一条对称轴,求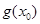 的值.
的值.
(2)求函数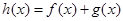 的单调递增区间.
的单调递增区间.
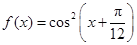 ,
,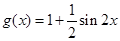 .
.(1)设
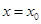 是函数
是函数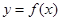 图象的一条对称轴,求
图象的一条对称轴,求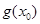 的值.
的值.(2)求函数
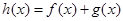 的单调递增区间.
的单调递增区间.(1)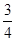 或
或 ,(2)
,(2)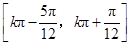 (
( ).
).
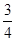 或
或 ,(2)
,(2)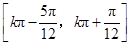 (
( ).
).试题分析:(1)先将三角函数化为基本三角函数,即利用降幂公式得
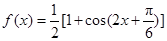 ,再利用基本三角函数性质得:
,再利用基本三角函数性质得:
 ,即
,即 ,所以
,所以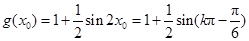 .因此分
.因此分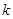 为奇偶讨论得,
为奇偶讨论得,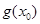 的值为
的值为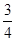 或
或 ,(2)同样先将三角函数化为基本三角函数,此时要用到两角和余弦公式及配角公式,即
,(2)同样先将三角函数化为基本三角函数,此时要用到两角和余弦公式及配角公式,即

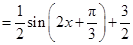 ,再利用基本三角函数性质得:
,再利用基本三角函数性质得: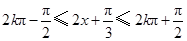 ,即
,即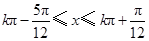 (
( ),故函数
),故函数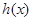 的单调递增区间是
的单调递增区间是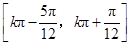 (
( ).
).试题解析:(1)由题设知
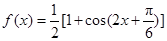 .
.因为
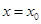 是函数
是函数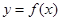 图象的一条对称轴,所以
图象的一条对称轴,所以
 ,
,即
 (
( ).所以
).所以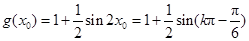 .
.当
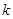 为偶数时,
为偶数时,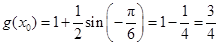 ,
,当
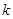 为奇数时,
为奇数时,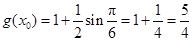 .
.(2)

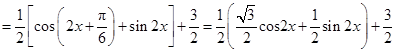
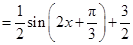 .
.当
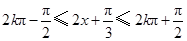 ,即
,即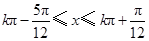 (
( )时,
)时,函数
 是增函数,
是增函数,故函数
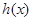 的单调递增区间是
的单调递增区间是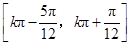 (
( ).
).
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
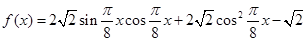 ,
,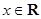 .
.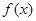 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;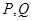 的横坐标依次为
的横坐标依次为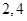 ,
,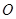 为坐标原点,求
为坐标原点,求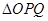 的外接圆的面积.
的外接圆的面积.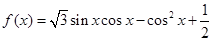 .
.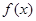 的最小正周期及对称轴方程;
的最小正周期及对称轴方程;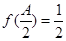 ,bc=6,求a的最小值.
,bc=6,求a的最小值.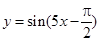 的图象向右平移
的图象向右平移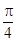 个单位,再把所得函数图象上各点的橫坐标缩短为原来的
个单位,再把所得函数图象上各点的橫坐标缩短为原来的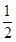 ,所得函数的解析式为( )
,所得函数的解析式为( )



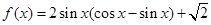 ,
,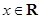 .
.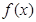 的最小正周期和单调增区间;
的最小正周期和单调增区间;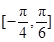 上的最小值和最大值;
上的最小值和最大值;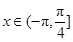 ,求使
,求使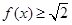 的
的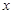 取值范围.
取值范围. 的图像,只须将
的图像,只须将 的图像 ( )
的图像 ( ) 个单位
个单位 个单位
个单位 取最大值时
取最大值时 的值为( )(以下的
的值为( )(以下的 )
)



 ,则函数
,则函数 的最大值为____________.
的最大值为____________.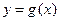 的图象由
的图象由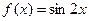 的图象向右平移
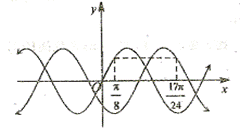
的图象向右平移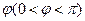 个单位得到,这两个函数的部分图象如图所示,则
个单位得到,这两个函数的部分图象如图所示,则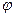 的值为( )
的值为( )