题目内容
在 中,
中, ,
, ,
, ,则最短边长为( )
,则最短边长为( )
A. | B. | C. | D. |
A
解析试题分析:因为 ,
, ,所以
,所以 ,即
,即 的对边b最短。由正弦定理得,
的对边b最短。由正弦定理得, ,选A。
,选A。
考点:本题主要考查三角形内角和定理,正弦定理的应用。
点评:简单题,三角形中“大角对大边,小角对小边”。

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
在△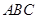 中,若
中,若 ,则△
,则△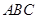 的形状是( )
的形状是( )
| A.钝角三角形 | B.直角三角形 | C.锐角三角形 | D.不能确定 |
在△ABC中, 所对的边分别为
所对的边分别为 ,则下列关系正确的是 ( )
,则下列关系正确的是 ( )
A. | B. |
C. | D. |
已知△ABC的面积为
 ,则角C的度数为( )
,则角C的度数为( )
A. | B. | C. | D. |
在 中,边
中,边 所对的角分别为
所对的角分别为 ,若
,若 ,则
,则 ( )
( )
A. | B. | C. | D. |
在 中,下列关系式不一定成立的是( )。
中,下列关系式不一定成立的是( )。
A. | B. |
C. | D. |
在⊿ABC中, ,则此三角形为( )
,则此三角形为( )
| A.直角三角形; | B.等腰直角三角形 |
| C.等腰三角形 | D.等腰或直角三角形 |
半径为4的球面上有 、
、 、
、 、
、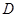 四点,
四点, 、
、 、
、 两两互相垂直,则 △
两两互相垂直,则 △ 、△
、△ 、△
、△ 面积和的最大值为 ( )
面积和的最大值为 ( )
| A.8 | B.16 | C.32. | D.64 |
在 中,
中, ,
, ,其面积为
,其面积为 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |