题目内容
已知集合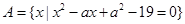 ,集合
,集合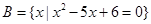 ,是否存在实数
,是否存在实数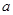 ,使得集合A、B能同时满足下列三个条件:
,使得集合A、B能同时满足下列三个条件:
①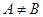 ;②
;②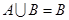 ;③
;③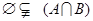 ?若存在,求出实数
?若存在,求出实数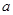 的值或取值范围;若不存在,请说明理由.
的值或取值范围;若不存在,请说明理由.
【答案】
这样的实数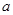 不存在
不存在
【解析】
试题分析:由已知条件可得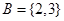 ,若存在,由
,若存在,由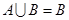 ,且
,且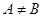 ,∴
,∴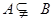 ,
,
又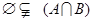 ,∴
,∴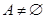 ,∴
,∴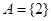 ,或
,或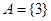 ,
,
当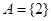 时,有
时,有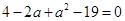 ,即
,即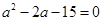 ,
,
解得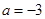 ,或
,或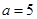 ,此时集合
,此时集合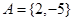 ,或
,或 都与
都与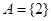 矛盾;
矛盾;
当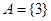 时,同理得出矛盾,故这样的实数
时,同理得出矛盾,故这样的实数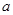 不存在.
不存在.
考点:本题主要考查子集、集合相等、交集、并集的概念、集合中元素的性质。
点评:此题考查了集合的各种运算,探究求得a,利用集合中元素的互异性,确认其是否存在性。

练习册系列答案
相关题目
 ,若集合
,若集合 ,且对任意的
,且对任意的 ,存在
,存在 ,使得
,使得 (其中
(其中 ),则称集合
),则称集合 为集合
为集合 的一个
的一个 元基底.
元基底.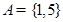 ,
, ;
; ,
, .
. ;
; 的一个
的一个 ,若集合
,若集合 ,且对任意的
,且对任意的 ,存在
,存在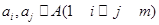 ,使得
,使得 (其中
(其中 ),则称集合
),则称集合 为集合
为集合 的一个
的一个 元基底.
元基底. ,
, ;
; ,
, .
. ;
; 的一个
的一个