题目内容
18.已知在△ABC中,内角A、B、C所对的边分别为a、b、c,且sin(A+$\frac{π}{6}$)=2cosA.(1)若cosC=$\frac{\sqrt{6}}{3}$,求证:2a-3c=0;
(2)若B∈(0,$\frac{π}{3}$),且cos(A-B)=$\frac{4}{5}$,求sinB的值.
分析 (1)化简sin(A+$\frac{π}{6}$)=2cosA可得tanA=$\sqrt{3}$,又A为三角形内角.可求sinA的值,又cosC=$\frac{\sqrt{6}}{3}$,C为三角形内角,可求sinC的值,由正弦定理可得:a=sinA•2R,c=sinC•2R,代入等式右边即可证明.
(2)由B∈(0,$\frac{π}{3}$),可求cosB=$\sqrt{1-si{n}^{2}B}$,由cos(A-B)=$\frac{4}{5}$,利用同角三角函数关系式化简即可求值.
解答 解:(1)证明:∵sin(A+$\frac{π}{6}$)=2cosA
⇒$\frac{\sqrt{3}}{2}$sinA+$\frac{1}{2}$cosA=2cosA
⇒sinA=$\sqrt{3}$cosA
⇒tanA=$\sqrt{3}$,A为三角形内角.
⇒A=$\frac{π}{3}$,sinA=$\frac{\sqrt{3}}{2}$
又∵cosC=$\frac{\sqrt{6}}{3}$,C为三角形内角,
∴sinC=$\sqrt{1-co{s}^{2}C}$=$\frac{\sqrt{3}}{3}$,
∵由正弦定理可得:a=sinA•2R,c=sinC•2R
∴2a-3c=2R×$2×\frac{\sqrt{3}}{2}$-3×$\frac{\sqrt{3}}{3}×2R$=2$\sqrt{3}R$-2$\sqrt{3}R$=0.从而得证.
(2)∵B∈(0,$\frac{π}{3}$),
∴A-B=$\frac{π}{3}$-B∈(0,$\frac{π}{3}$),
∵sin2(A-B)+cos2(A-B)=1,cos(A-B)=$\frac{4}{5}$,
∴sin(A-B)=$\frac{3}{5}$,
则sinB=sin[A-(A-B)]=sinAcos(A-B)-cosAsin(A-B)=$\frac{\sqrt{3}}{2}×\frac{4}{5}$-$\frac{1}{2}×\frac{3}{5}$=$\frac{4\sqrt{3}-3}{10}$.
点评 本题主要考查了同角三角函数关系式,三角函数恒等变换的应用,属于基本知识的考查.

| A. | 40% | B. | 50% | C. | 60% | D. | $\frac{2}{3}$ |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
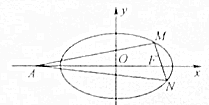 已知定点A的坐标是(-4,0),椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{6}}{3}$,F为椭圆的右焦点,M,N两点在椭圆C上,且$\overrightarrow{MF}$=$\overrightarrow{FN}$
已知定点A的坐标是(-4,0),椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{6}}{3}$,F为椭圆的右焦点,M,N两点在椭圆C上,且$\overrightarrow{MF}$=$\overrightarrow{FN}$