题目内容
函数 ( )
( )
A.是偶函数,且在 上是单调减函数 上是单调减函数 |
B.是奇函数,且在 上是单调减函数 上是单调减函数 |
C.是偶函数,且在 上是单调增函数 上是单调增函数 |
D.是奇函数,且在 上是单调增函数 上是单调增函数 |
D
解析试题分析:令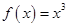 ,其定义域为
,其定义域为 ,因为
,因为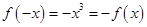 ,所以函数
,所以函数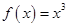 是奇函数。
是奇函数。
在 上任取两个实数
上任取两个实数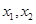 ,且
,且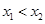 ,则
,则 ,因为
,因为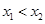 ,所以
,所以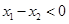 ,所以
,所以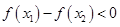 ,即
,即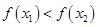 ,所以
,所以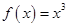 在
在 上单调递增。
上单调递增。
考点:1函数奇偶性;2函数单调性的定义。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设 ,则
,则 ( )
( )
A. | B.2 | C.3 | D.4 |
函数 的定义域为( )
的定义域为( )
A. | B. | C. | D. |
定义在R上的偶函数f(x)在(0,+∞)上是增函数,且f( )=0,则不等式
)=0,则不等式 的解集是( )
的解集是( )
A.(0, ) ) | B.( ,+∞) ,+∞) |
C.(- ,0)∪( ,0)∪( ,+∞) ,+∞) | D.(-∞,- )∪(0, )∪(0, ) ) |
设二次函数f(x)=x2+bx+c,满足f(x+3)=f(3-x),则使f(x)>c-8的x的取值范围为( )
| A.(-∞,2) | B.(4,+∞) |
| C.(-∞,2)∪(4,+∞) | D.(2,4) |
对实数a和b,定义运算“?”:a?b=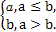 设函数f(x)=(x2-1)?(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )
设函数f(x)=(x2-1)?(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )
A.(-∞,-1)∪(- ,0) ,0) | B.{-1,- } } |
C.(-1,- ) ) | D.(-∞,-1)∪[- ,0) ,0) |
若不等式x2+ax+1≥0对于一切x∈(0, ]恒成立,则a的最小值是( )
]恒成立,则a的最小值是( )
| A.0 | B.2 | C.- | D.-3 |
