题目内容
（2013•和平区一模）已知命题p：关于x的函数f（x）=2x2+ax-1在[3，+∞）上是增函数；命题q：关于x的方程x2-ax+4=0有实数根．若pVq为真命题，p∧q为假命题，则实数a的取值范围是（ ）
分析：根据一元二次函数的单调区间求出命题P为真命题的条件，利用解不等式求得一元二次方程存在实数根的条件；
再根据复合命题真值表判断求解即可
再根据复合命题真值表判断求解即可
解答：解：∵函数f（x）=2x2+ax-1在[3，+∞）上是增函数，∴-
≤3⇒a≥-12，
∴命题P为真命题的条件是：a≥-12；
∵关于x的方程x2-ax+4=0有实数根，∴△=a2-16≥0⇒a≥4或a≤-4，
∴命题q为真命题的条件是：a≥4或a≤-4；
∵pVq为真命题，p∧q为假命题，根据复合命题的真值表，命题P、命题q一真一假
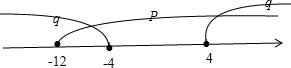
∴a＜-12或-4＜a＜4，
故选C
| a |
| 4 |
∴命题P为真命题的条件是：a≥-12；
∵关于x的方程x2-ax+4=0有实数根，∴△=a2-16≥0⇒a≥4或a≤-4，
∴命题q为真命题的条件是：a≥4或a≤-4；
∵pVq为真命题，p∧q为假命题，根据复合命题的真值表，命题P、命题q一真一假
∴a＜-12或-4＜a＜4，
故选C
点评：本题借助考查复合命题的真假判定，考查了一元二次函数的单调区间及一元二次方程存在根的判定．
练习册系列答案
相关题目
（2013•和平区一模）在如图所示的计算1+3+5+…+2013的值的程序框图中，判断框内应填入（ ）