题目内容
设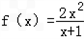 ,g(x)=ax+5﹣2a(a>0).
,g(x)=ax+5﹣2a(a>0).
(1)求f(x)在x∈[0,1]上的值域;
(2)若对于任意x1∈[0,1],总存在x0∈[0,1],使得g(x0)=f(x1)成立,求a的取值范围.
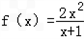 ,g(x)=ax+5﹣2a(a>0).
,g(x)=ax+5﹣2a(a>0).(1)求f(x)在x∈[0,1]上的值域;
(2)若对于任意x1∈[0,1],总存在x0∈[0,1],使得g(x0)=f(x1)成立,求a的取值范围.
解:(1)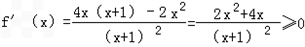 在x∈[0,1]上恒成立.
在x∈[0,1]上恒成立.
∴f(x)在[0,1]上增,
∴f(x)值域[0,1].
(2)f(x)值域[0,1],g(x)=ax+5﹣2a(a>0)在x∈[0,1]上的值域[5﹣2a,5﹣a].
由条件,只须[0,1]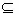 [5﹣2a,5﹣a].
[5﹣2a,5﹣a].
∴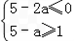
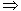
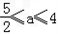 .
.
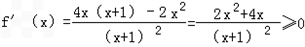 在x∈[0,1]上恒成立.
在x∈[0,1]上恒成立.∴f(x)在[0,1]上增,
∴f(x)值域[0,1].
(2)f(x)值域[0,1],g(x)=ax+5﹣2a(a>0)在x∈[0,1]上的值域[5﹣2a,5﹣a].
由条件,只须[0,1]
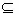 [5﹣2a,5﹣a].
[5﹣2a,5﹣a].∴
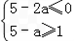
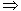
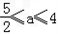 .
.
练习册系列答案
相关题目