题目内容
已知等差数列{an}的首项a1＝21，公差d＝－4．
(1)若|a1|＋|a2|＋…＋|ak|＝102，求k的值．
(2)设{an}的前n项和为Sn，试问数列{Sn}中是否存在相同的两项．若存在，求出这样的两项，若不存在，说明理由．
答案：
解析：
解析：
|
解：(1)易知k＝10． (2)因为Sn＝－2n2＋23n，假设Sp＝Sr， 则－2p2＋23p＝－2r2＋23r |
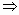2(r2－p2)＝23(r－p)．因为p≠r，所以p＋r＝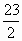
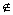N．因为p、r∈N，所以p＋r∈N．故这样的p，r不存在．
练习册系列答案
相关题目
a
的首项a
＝1，前n项和为s
．且对任意正整数n有n，a
，s
成等差
a
通项a
，Tn＝b1＋b2＋……＋bn，求Tn