题目内容
半径为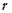
的球在一个圆锥内部，它的轴截面是一个正三角形与其内切圆，则圆锥的全面积与球面面积的比是 ( )
| A．2∶3 | B．3∶2 | C．4∶9 | D．9∶4 |
D
解析试题分析：因为球的半径为r，所以球面面积为：
。因为轴截面是一个正三角形与其内切圆，所以圆锥的底面半径为
，母线长为
，所以圆锥的侧面积为
，所以圆锥的全面积为
，所以圆锥的全面积与球面面积的比是9∶4。
考点：球的表面积公式；圆锥的侧面积公式。
点评：根据球的半径计算出圆锥的底面半径和母线长是解题的关键，也是解题的难点所在。我们可以结合图形进行分析。属于中档题。
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列几何体各自的三视图中,有且仅有两个视图相同的是( )
①正方体 ②圆锥 ③正三棱台 ④正四棱锥
| A．①② | B．①③ | C．①③ | D．②④ |
过空间任意一点引三条不共面的直线，它们所确定的平面个数是( )
| A．1 | B．2 | C．3 | D．1或3 |
。则该几何体的俯视图可以是（ ）
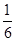
的等腰三角形,侧视图是半径为1的半圆，则该几何体的体积是（ ）
