题目内容
在三棱锥S—ABC中,∠SAB=∠SAC=∠ACB=90°,AC=2,BC=(Ⅰ)证明:SC⊥BC;
(Ⅱ)求侧面SBC与底面ABC所成二面角的大小;
(Ⅲ)求异面直线SC与AB所成的角的大小(用反三角函数表示).
答案:
解析:
解析:
| (Ⅰ)证明:∵∠SAB=∠SAC=90°,
∴SA⊥AB,SA⊥AC.
又AB∩AC=A, ∴SA⊥平面ABC. 由于∠ACB=90°,即BC⊥AC, 由三垂线定理,得SC⊥BC. (Ⅱ)解:∵BC⊥AC,SC⊥BC, ∴∠SCA是侧面SCB与底面ABC所成二面角的平面角. 在Rt△SCB中,由BC= SC= 在Rt△SAC中,由AC=2,SC=4,得cosSCA= ∴∠SCA=60°,即侧面SBC与底面ABC所成二面角的大小为60°. (Ⅲ)解:过点C作CD∥BA,过点A作BC的平行线交CD于D,连结SD,则∠SCD是异面直线SC与AB所成的角.如图. 又四边形ABCD是平行四边形, DC=AB= SA= SD= 在△SCD中,cosSCD= ∴SC与AB所成的角的大小为arccos |

练习册系列答案
相关题目

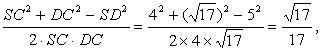
 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.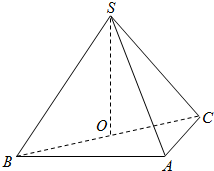 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点. 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2, C.
C. 如图,在三棱锥S-ABC中,
如图,在三棱锥S-ABC中,