题目内容
已知函数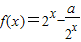 ,将y=f(x)的图象向右平移两个单位,得到y=g(x)的图象.
,将y=f(x)的图象向右平移两个单位,得到y=g(x)的图象.(1)求函数y=g(x)的解析式;
(2)若函数y=h(x)与函数y=g(x)的图象关于直线y=1对称,求函数y=h(x)的解析式;
(3)设
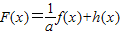 ,设F(x)的最小值为m.是否存在实数a,使
,设F(x)的最小值为m.是否存在实数a,使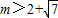 ,若存在,求出a的取值范围,若不存在,说明理由.
,若存在,求出a的取值范围,若不存在,说明理由.
【答案】分析:(1)根据坐标平移的规律左加右减得到g(x)的解析式;
(2)设出h(x)上任一点的坐标求出关于y=1对称点的坐标代入g(x)求出h(x)的解析式即可;
(3)根据已知先求出F(x)的解析式,分四种情况讨论a的取值,因为F(x)的最小值是m,所以只有当 <a<4时,根据不等式的基本性质求出F(x)的最小值等于m,又根据m>2+
<a<4时,根据不等式的基本性质求出F(x)的最小值等于m,又根据m>2+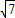 ,列出不等式组求出解集即可.
,列出不等式组求出解集即可.
解答:解:(1)∵函数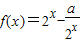 ,将y=f(x)的图象向右平移两个单位,得到y=g(x)的图象,
,将y=f(x)的图象向右平移两个单位,得到y=g(x)的图象,
g(x)=f(x-2)=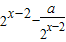 ;
;
(2)设y=h(x)上的任意点P(x,y),则P关于y=1对称点为Q(x,2-y),点Q在y=g(x)上,所以h(x)=2-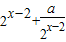 ;
;
(3)F(x)=(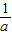 -
- )2x+(4a-1)
)2x+(4a-1)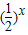 +2
+2
①当a<0时,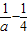 <0,4a-1<0,∴F(x)<2,与题设矛盾
<0,4a-1<0,∴F(x)<2,与题设矛盾
②当0<a≤ 时,
时,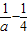 >0,4a-1≤0,F(x)在R上是增函数,F(x)无最小值;
>0,4a-1≤0,F(x)在R上是增函数,F(x)无最小值;
③当a≥4时,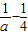 ≤0,4a-1>0,F(x)在R上是减函数,F(x)无最小值
≤0,4a-1>0,F(x)在R上是减函数,F(x)无最小值
④当 <a<4时,
<a<4时,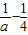 >0,4a-1>0,F(x)≥2
>0,4a-1>0,F(x)≥2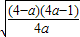 +2=m
+2=m
由m>2+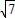 ,得
,得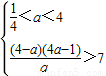 ,
,
∴1<a<4
点评:本题考查函数的解析式,考查图象的平移,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.
(2)设出h(x)上任一点的坐标求出关于y=1对称点的坐标代入g(x)求出h(x)的解析式即可;
(3)根据已知先求出F(x)的解析式,分四种情况讨论a的取值,因为F(x)的最小值是m,所以只有当
 <a<4时,根据不等式的基本性质求出F(x)的最小值等于m,又根据m>2+
<a<4时,根据不等式的基本性质求出F(x)的最小值等于m,又根据m>2+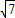 ,列出不等式组求出解集即可.
,列出不等式组求出解集即可.解答:解:(1)∵函数
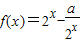 ,将y=f(x)的图象向右平移两个单位,得到y=g(x)的图象,
,将y=f(x)的图象向右平移两个单位,得到y=g(x)的图象,g(x)=f(x-2)=
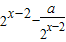 ;
;(2)设y=h(x)上的任意点P(x,y),则P关于y=1对称点为Q(x,2-y),点Q在y=g(x)上,所以h(x)=2-
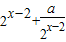 ;
;(3)F(x)=(
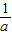 -
- )2x+(4a-1)
)2x+(4a-1)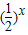 +2
+2①当a<0时,
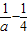 <0,4a-1<0,∴F(x)<2,与题设矛盾
<0,4a-1<0,∴F(x)<2,与题设矛盾②当0<a≤
 时,
时,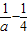 >0,4a-1≤0,F(x)在R上是增函数,F(x)无最小值;
>0,4a-1≤0,F(x)在R上是增函数,F(x)无最小值;③当a≥4时,
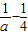 ≤0,4a-1>0,F(x)在R上是减函数,F(x)无最小值
≤0,4a-1>0,F(x)在R上是减函数,F(x)无最小值④当
 <a<4时,
<a<4时,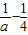 >0,4a-1>0,F(x)≥2
>0,4a-1>0,F(x)≥2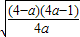 +2=m
+2=m由m>2+
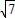 ,得
,得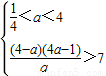 ,
,∴1<a<4
点评:本题考查函数的解析式,考查图象的平移,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 ,在y轴右侧的第一个最高点的横坐标为
,在y轴右侧的第一个最高点的横坐标为 .
. 个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的最大值及单调递减区间.
个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的最大值及单调递减区间.