Question

设H是△ABC 的外心，A（1，0），B（-1，0），O为坐标原点，动点G满足：3=+，且=λ,λ∈R.

（1）求顶点C的轨迹E的方程；

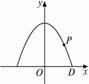
（2）如图，从点D（，0）发射出一个质点m沿抛物线C₁：y=-ax²+h向上飞行到点P时,立即得到变轨指令，即开始沿着曲线E运动.两曲线C₁和E在公共点P处的切线相同.求抛物线C₁的方程.

Answer 1

解:（1）令=(x₁,y₁),=(x,y),则=(x+1,y),                                    

由3=+得?

3=3(x₁,y₁)=(1,0)+(x+1,y)=(x+2,y),?

∴3y₁=y.?

又=λ,λ∈R.?

∴GH∥AB.?

∴H(0,).                                                                                                              ?

∵H是△ABC的外心，?

∴|HA|=|HC|.?

∴=(y≠0).?

整理得x²+=1(y≠0).                                                                                    

（2）设P（x₀,y₀）,∵y=-ax²+h.?

∴y′=-2ax,在P处的切线斜率为-2ax₀.?

对于椭圆，当y＞0时，y=,y′=,?

在P处的切线斜率为,?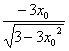

∴-2ax₀=-.                                                                                              ?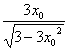

①当x₀≠0时，x₀²=,y₀=.?

又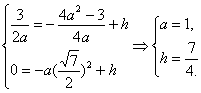

∴抛物线方程为y=-x²+.                                                                                      ?

②当x₀=0时，y₀=,点（0,）在抛物线上，则=h;点(,0)在抛物线上，?

∴0=-a()+h.∴a=.?

∴y=-x²+.