题目内容
某工厂要建造一个无盖长方体水池,底面一边长固定为8 m,最大装水量为72 m3,池底和池壁的造价分别为2a元/m2、a元/m2,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
答案:
解析:
解析:
|
答:将水池底的矩形另一边和长方体高都设计为3 m时,总造价最低,最低造价为51a元. 解:设池底一边长为x,水池的高为y,池底、池壁造价分别为z1,z2,则总造价为z=z1+z2 由最大装水量知 当且仅当 |

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
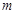 ,最大装水量为72
,最大装水量为72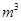 ,池底和池壁的造价分别为
,池底和池壁的造价分别为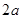 元
元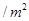 、
、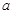 元
元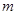 ,最大装水量为72
,最大装水量为72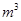 ,池底和池壁的造价分别为
,池底和池壁的造价分别为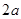 元
元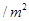 、
、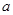 元
元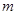 ,最大装水量为72
,最大装水量为72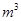 ,池底和池壁的造价分别为
,池底和池壁的造价分别为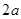 元
元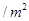 、
、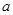 元
元