题目内容
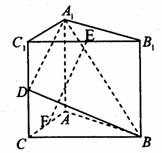
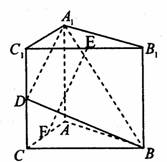
如下图,在直三棱柱ABC—A1B1C1中，AC＝3，BC＝4，AA1＝4，AB=5,点D是AB的中点，
（1）求证：AC1∥平面CDB1；
（2）求异面直线AC1与B1C所成角的余弦值．
思路解析：本题第一问要证明直线与平面平行,可以围绕着线面平行的判定定理,转而去证明线线平行,结合已知条件不难得以证明;第二问是要求异面直线所成的角,就要考虑平移其中一条（或两条）直线,从而转化为相交两直线所成的角的问题,从而得以求解.
(1)证明：设CB1与C1B的交点为E，连结DE.
∵D是AB的中点，E是BC1的中点，
∴DE∥AC1.
∵DE
平面CDB1,AC1
平面CDB1,
∴AC1∥平面CDB1.
（2）解：∵DE∥AC1,∴∠CED为AC1与B1C所成的角.
在△CED中，ED=
AC1=
,CD=
AB=
，CE=
CB1=2
,
∴由余弦定理得
cos∠CED=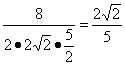
.
∴异面直线AC1与B1C所成角的余弦值为
.
练习册系列答案
相关题目
，底面三角形的三边长分别为3a、4a、5a(a＞0)．用它们拼成一个三棱柱或四棱柱，在所有可能的情形中，全面积最小的是一个四棱柱，则a的取值范围是________
，底面三角形的三边长分别为3a、4a、5a(a＞0)．用它们拼成一个三棱柱或四棱柱，在所有可能的情况中，全面积最小的是一个四棱柱，则a的取值范围是________．
