题目内容
已知双曲线的一个焦点与虚轴的一个端点的连线及实轴所在直线所成的角为30°,则双曲线的离心率为
.
| ||
| 2 |
| ||
| 2 |
分析:根据已知条件,求出b与c的关系,利用c2=a2+b2,求出双曲线的离心率.
解答:解:根据双曲线的一个焦点与虚轴的一个端点的连线及实轴所在直线所成的角为30°,
∴c=
b,
∴c2=3b2,∴3c2-3a2=c2
∴e=
.
故答案为:
.
∴c=
| 3 |
∴c2=3b2,∴3c2-3a2=c2
∴e=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题主要考查了双曲线的简单性质.本题利用了双曲线的离心率的求法,考查计算能力.

练习册系列答案
相关题目
已知双曲线的一个焦点与抛物线x2=20y的焦点重合,且其渐近线的方程为3x±4y=0,则该双曲线的标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为
,则该双曲线的方程为
 B.
B.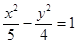 C.
C. D.
D.