题目内容

 已知4个命题：

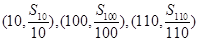①若等差数列的前n项和为则三点共线；

②命题：“”的否定是“”；

③若函数在（0，1）没有零点，则k的取值范围是

④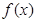是定义在R上的奇函数，的解集为（2，2）

其中正确的是     。

 

【答案】

①②④

【解析】

试题分析：①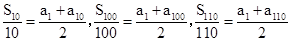，设等差数列的公差为d，

∴

，

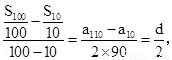
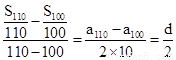即 前两个点连线的斜率等于后两个点连线的斜率，故三点共线，故①正确．

②根据命题的否定的定义，“?x∈R，x2+1＞3x”的否定是“?x∈R，x2+1≤3x”；是正确的，故②正确．

③函数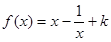在（0，1）没有零点，故f′（x）=1+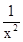＞0，所以函数在（0，1）内是增函数，x-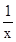＜0，当k≥2时，函数有零点，③不正确．

④f（x）是定义在R上的奇函数，f′（x）＞0，且f（2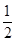）=，所以x＞0时，函数是恒为正值，f（0）=0，x＜0时函数为负值，2f（2）=1，则xf（x）＜1的解集为（-2，2）．正确．

故答案为：①②④．

考点：本题主要考查利用导数研究函数的单调性；命题的否定；函数零点的判定定理；三点共线．

点评：综合题，考查三点共线，命题的否定，零点，导数与不等式的知识，考查知识的灵活应用能力，属中档题．

 

练习册系列答案
相关题目
已知4个命题：
①若等差数列{an}的前n项和为Sn则三点（10，
S10
10
），（100，
S100
100
），（110，
S110
110
），共线；
②命题：“?x∈R，x2+1＞3x”的否定是“?x∈R，x2+1≤3x”；
③若函数f（x）=x-
1
x
+k在（0，1）没有零点，则k的取值范围是k≥2，
④f（x）是定义在R上的奇函数，f′（x）＞0，且f（2）=
1
2
，则xf（x）＜1的解集为（-2，2）．
其中正确的是
 
．
已知4个命题：
①若等差数列{an}的前n项和为Sn则三点（10，
S10
10
），（100，
S100
100
），（110，
S110
110
），共线；
②命题：“?x∈R，x2+1＞3x”的否定是“?x∈R，x2+1≤3x”；
③若函数f（x）=x-
1
x
+k在（0，1）没有零点，则k的取值范围是k≥2，
④f（x）是定义在R上的奇函数，f′（x）＞0，且f（2）=
1
2
，则xf（x）＜1的解集为（-2，2）．
其中正确的是______．
已知4个命题：
①若等差数列{an}的前n项和为Sn则三点（10，），（100，），（110，），共线；
②命题：“?x∈R，x2+1＞3x”的否定是“?x∈R，x2+1≤3x”；
③若函数f（x）=x-+k在（0，1）没有零点，则k的取值范围是k≥2，
④f（x）是定义在R上的奇函数，f′（x）＞0，且f（2）=，则xf（x）＜1的解集为（-2，2）．
其中正确的是    ．

已知4个命题：

　 ①若等差数列{}的前n项和为，则三点（10,），（100,），（110,）共线；

　 ②命题“∈R，使得＋1＞3x”的否定是“∈R，＋1≤3x”；

　 ③若函数f（x）＝x－＋k在（0，1）没有零点，则k的取值范围是k≥2；

③f（x）是定义在R上的奇函数（x）>0，且f（2）＝，则xf（x）<1的解集为（－2，2）．

　 其中正确的是_____________．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网