题目内容
21.已知有穷数列(1)求证:数列![]()
![]()
![]() 是等比数列;
是等比数列;
(2)若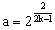 ,数列
,数列![]()
![]()
![]() 满足
满足![]() =
=![]() (
(![]() =1,2,┅,2
=1,2,┅,2![]() ),求数列
),求数列![]()
![]()
![]() 的通项公式;
的通项公式;
(3)若(2)中的数列![]()
![]()
![]() 满足不等式|
满足不等式|![]() -
-![]() |+|
|+|![]() -
-![]() |+┅+|
|+┅+|![]() -
-![]() |+|
|+|![]() -
-![]() |≤4,求
|≤4,求![]() 的值.
的值.
解:(1)![]() ,则
,则![]() ,两式相减,得
,两式相减,得![]() ,(又
,(又![]() )
)
∴数列![]()
![]()
![]() 是首项为
是首项为![]() 、公比为
、公比为![]() 的等比数列。
的等比数列。
(2)![]() =
=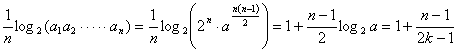 ,
,
(![]() =1,2,┅,2
=1,2,┅,2![]() )。
)。
(3)由(2)知,数列![]()
![]()
![]() 是首项为
是首项为![]() 、公差为
、公差为![]() 的等差数列。
的等差数列。
又![]() ,∴
,∴![]() 时,
时,![]() ;
;![]() 时,
时,![]() 。
。
∴|![]() -
-![]() |+|
|+|![]() -
-![]() |+┅+|
|+┅+|![]() -
-![]() |+|
|+|![]() -
-![]() |
|![]()
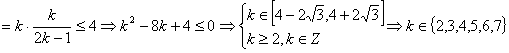 。
。

练习册系列答案
相关题目