题目内容
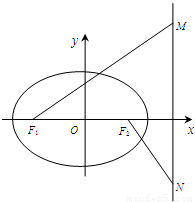
如图，椭圆
（a＞b＞0）的一个焦点是F（1，0），O为坐标原点。
（a＞b＞0）的一个焦点是F（1，0），O为坐标原点。
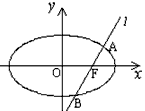
（1）已知椭圆短轴的两个三等分点与一个焦点构成正三角形，求椭圆的方程；
（2）设过点F的直线l交椭圆于A、B两点。若直线l绕点F任意转动，恒有|OA|2+|OB|2＜|AB|2，求a的取值范围。
（2）设过点F的直线l交椭圆于A、B两点。若直线l绕点F任意转动，恒有|OA|2+|OB|2＜|AB|2，求a的取值范围。
解：（1）设M，N为短轴的两个三等分点，因为△MNF为正三角形
所以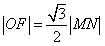
即1=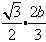
解得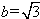
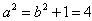
因此，椭圆方程为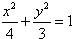
；
所以
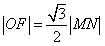
即1=
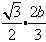
解得
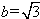
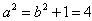
因此，椭圆方程为
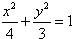；（2）设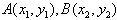
（i）当直线AB与x轴重合时
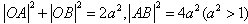
因此，恒有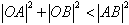
。
（ii）当直线AB不与x轴重合时，
设直线AB的方程为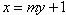
代入
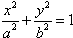
整理得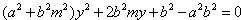
所以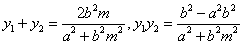
因为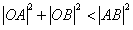
所以∠AOB恒为钝角
即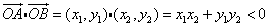
恒成立
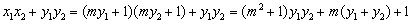
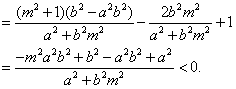
又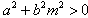
所以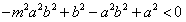
对m∈R恒成立，
即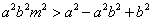
对m∈R成立
当m∈R时，
最小值为0
所以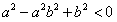
因为a>0，b>0
所以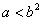
即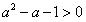
解得a＞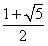
或a＜
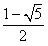（舍去）
即a＞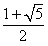
综合（i）（ii），a的取值范围为（，+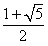
）。
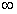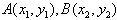
（i）当直线AB与x轴重合时
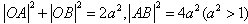
因此，恒有
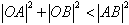。（ii）当直线AB不与x轴重合时，
设直线AB的方程为
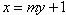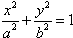
代入整理得
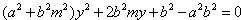
所以
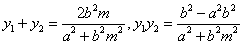
因为
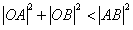
所以∠AOB恒为钝角
即
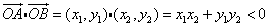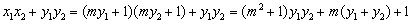
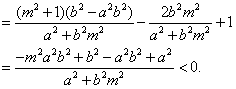
恒成立又
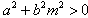
所以
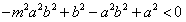对m∈R恒成立， 即
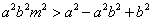对m∈R成立当m∈R时，
最小值为0所以
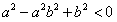
因为a>0，b>0
所以
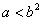
即
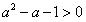
解得a＞
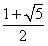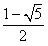或a＜（舍去）即a＞
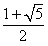
综合（i）（ii），a的取值范围为（
，+）。
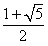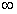练习册系列答案
相关题目
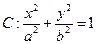（a＞b＞0）的一个焦点为F(1,0)，且过点（2，0）.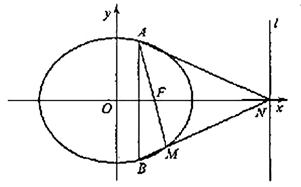
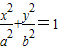（a＞b＞0）的一个焦点为F(1,0)，且过点（2，0）.（Ⅰ）求椭圆C的方程；（Ⅱ）若AB为垂直于x轴的动弦，直线
与
轴交于点N，直线AF与BN交于点
．求证：点M恒在椭圆C上．
（a＞b＞0）的一个焦点为F(1,0)，且过点（2，0）.
=1(a＞b＞c)的右准线l与x轴的交点为A，椭圆的上顶点为B，过椭圆的右焦点F作垂直于椭圆长轴的直线交椭圆于P点.若点D满足
(λ≠0).
（a＞b＞0）过点
，其左、右焦点分别为F1，F2，离心率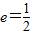
，M，N是椭圆右准线上的两个动点，且
．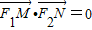