题目内容
(22) (本小题满分14分)
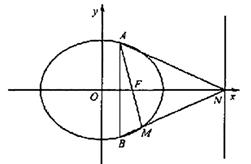
如图,椭圆![]() (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M.
(ⅰ)求证:点M恒在椭圆C上;
(ⅱ)求△AMN面积的最大值.

(1)椭圆C方程为![]() .(2)同解析
.(2)同解析
解析:
解法一:
(Ⅰ)由题设a=2,c=1,从而b2=a2-c2=3,
所以椭圆C方程为![]() .
.
(Ⅱ)(i)由题意得F(1,0),N(4,0).
设A(m,n),则B(m,-n)(n≠0),![]() =1. ……①
=1. ……①
AF与BN的方程分别为:n(x-1)-(m-1)y=0,
n(x-4)-(m-4)y=0.
![]() 设M(x0,y0),则有 n(x0-1)-(m-1)y0=0, ……②
设M(x0,y0),则有 n(x0-1)-(m-1)y0=0, ……②
n(x0-4)+(m-4)y0=0, ……③
由②,③得
x0=![]() .
.
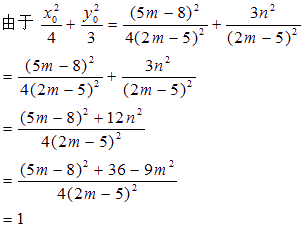
所以点M恒在椭圆G上.
(ⅱ)设AM的方程为x=xy+1,代入![]() =1得(3t2+4)y2+6ty-9=0.
=1得(3t2+4)y2+6ty-9=0.
设A(x1,y1),M(x2,y2),则有:y1+y2=![]()
|y1-y2|=![]()
令3t2+4=λ(λ≥4),则
|y1-y2|=![]()
因为λ≥4,0<![]()
|y1-y2|有最大值3,此时AM过点F.
△AMN的面积S△AMN=![]()
解法二:
(Ⅰ)问解法一:
(Ⅱ)(ⅰ)由题意得F(1,0),N(4,0).
设A(m,n),则B(m,-n)(n≠0), ![]() ……①
……①
AF与BN的方程分别为:n(x-1)-(m-1)y=0, ……②
n(x-4)-(m-4)y=0, ……③
由②,③得:当≠![]() . ……④
. ……④
由④代入①,得![]() =1(y≠0).
=1(y≠0).
当x=![]() 时,由②,③得:
时,由②,③得: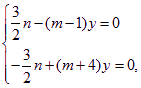
解得![]() 与a≠0矛盾.
与a≠0矛盾.
所以点M的轨迹方程为![]() 即点M恒在锥圆C上.
即点M恒在锥圆C上.
(Ⅱ)同解法一.

 阅读快车系列答案
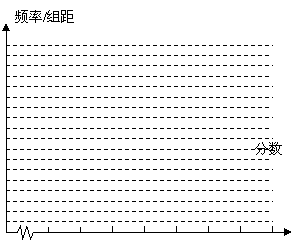
阅读快车系列答案(本小题12分)某次测试有900人参加,满分为100分,为了了解成绩情况,抽取了50名同学的成绩进行统计.
(1) 将频率分布表补充完整; (2) 绘制频率分布直方图;
(3) 估计全体学生中及格(不低于60分)的人数大约是多少.
| 分 组 | 频数 | 频率 |
| [40,50) | 4 | |
| [50,60) | 0.12 | |
| [60,70) | 9 | |
| [70,80) | 15 | |
| [80,90) | 0.22 | |
| [90,100) | ||
| 合 计 | 50 |
 |