题目内容
【题目】已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程.
(2)点P在直线l:2x-4y+3=0上,过点P作圆C的切线,切点记为M,求使|PM|最小的点P的坐标.
【答案】(1) (2+![]() )x-y=0或(2-
)x-y=0或(2-![]() )x-y=0或x+y+1=0或x+y-3=0
)x-y=0或x+y+1=0或x+y-3=0
(2) (-![]() ,
,![]() )
)
【解析】(1)将圆C的方程整理,得(x+1)2+(y-2)2=2.
①当切线在两坐标轴上的截距为零时,设切线方程为y=kx,
则![]() ,解得k=2±
,解得k=2±![]() ,
,
从而切线方程为y=(2±![]() )x.
)x.
②当切线在两坐标轴上的截距不为零时,设切线方程为x+y-a=0,则![]() ,解得a=-1或3,
,解得a=-1或3,
从而切线方程为x+y+1=0或x+y-3=0.
综上,切线方程为(2+![]() )x-y=0或(2-
)x-y=0或(2-![]() )x-y=0或x+y+1=0或x+y-3=0.
)x-y=0或x+y+1=0或x+y-3=0.
(2)因为圆心C(-1,2)到直线l的距离d=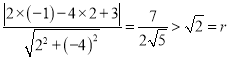 ,所以直线l与圆C相离.
,所以直线l与圆C相离.
当|PM|取最小值时,|CP|取得最小值,此时CP垂直于直线l.
所以直线CP的方程为2x+y=0.
解方程组![]() 得点P的坐标为(-
得点P的坐标为(-![]() ,
,![]() ).
).

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目