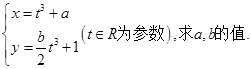题目内容
已知直线l经过点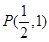
，倾斜角α＝
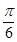，圆C的极坐标方程为
.
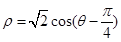(1)写出直线l的参数方程，并把圆C的方程化为直角坐标方程；
(2)设l与圆C相交于两点A、B，求点P到A、B两点的距离之积．
（1）
；（2）
.
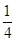解析试题分析：（1）由参数方程的概念可以写成l的参数方程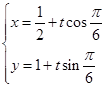为
，化简为
(t为参数) ；在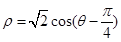两边同时乘以
，且ρ2＝x2＋y2，ρcosθ＝x，ρsinθ＝y，∴.（2）在l取一点，用参数形式表示，再代入，得到t2＋
t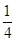－＝0，|PA|·|PB|＝|t1t2|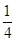＝.故点P到点A、B两点的距离之积为.
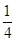试题解析：(1)直线l的参数方程为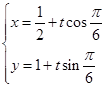,即 (t为参数)
由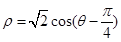,得ρ＝cosθ＋sinθ，所以ρ2＝ρcosθ＋ρsinθ，
∵ρ2＝x2＋y2，ρcosθ＝x，ρsinθ＝y，∴.
(2)把代入.
得t2＋t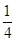－＝0，|PA|·|PB|＝|t1t2|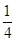＝.故点P到点A、B两点的距离之积为.
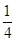考点：1.参数方程的应用；2.极坐标方程与直角坐标方程的转化.
练习册系列答案
黄冈小状元解决问题天天练系列答案
相关题目
(φ为参数),曲线C2的参数方程为
(a>b>0,φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=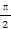
时,这两个交点重合.
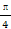时,l与C1,C2的交点分别为A1,B1,当α=-
，直线
的参数方程为
（t为参数，
） 
，求直线
(φ为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程是ρ＝2.正方形ABCD的顶点都在C2上，且A，B，C，D依逆时针次序排列，点A的极坐标为
，
，半径R＝
，求圆C的极坐标方程．
，直线
，以O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系.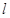
方程化为极坐标方程；
，当点P在
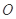为极点，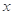
轴的非负半轴为极轴建立极坐标系．已知点
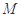的极坐标为
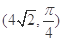，曲线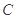
的参数方程为
（
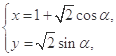为参数）．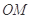
的直角坐标方程；
中以
为极点，
轴正半轴为极轴建立坐标系.圆
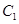，直线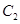
的极坐标方程分别为
.
