题目内容
已知点H(-3,0),点P在y轴上,点Q在x轴正半轴上,点M在直线PQ上,且满足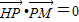 ,
,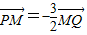 .
.(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过点(1,0)作直线L交轨迹C于A、B两点,已知
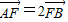 ,求直线L的方程.
,求直线L的方程.
【答案】分析:(1)设出M的坐标,利用题意向量的关系,求得x和y的关系,进而求得M的轨迹C.
(2)设出A,B的坐标,利用知 ,求出A,B的坐标,即可求直线L的方程
,求出A,B的坐标,即可求直线L的方程
解答:解:(1)设点M的坐标为(x,y),
由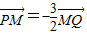 得P(0,-
得P(0,- ),Q(
),Q( ,0),
,0),
由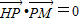 得(3,-
得(3,- )•(x,
)•(x,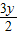 )=0,
)=0,
所以y2=4x由点Q在x轴的正半轴上,得x>0,
所以,动点M的轨迹C是以(0,0)为顶点,以(1,0)为焦点的抛物线,除去原点;
(2)设A(x1,y1),B(x2,y2),则
∵ ,∴(1-x1,-y1)=2(x2-1,y2),
,∴(1-x1,-y1)=2(x2-1,y2),
∴x1+2x2=3,y1=-2y2,
∵y12=4x1,y22=4x2,
∴x1=2,y1=±
∴直线L的方程为y=±2 (x-1).
(x-1).
点评:本题以向量得数量积得坐标表示为载体考查了轨迹方程,考查学生的计算能力,属于中档题.
(2)设出A,B的坐标,利用知
 ,求出A,B的坐标,即可求直线L的方程
,求出A,B的坐标,即可求直线L的方程解答:解:(1)设点M的坐标为(x,y),
由
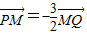 得P(0,-
得P(0,- ),Q(
),Q( ,0),
,0),由
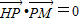 得(3,-
得(3,- )•(x,
)•(x,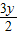 )=0,
)=0,所以y2=4x由点Q在x轴的正半轴上,得x>0,
所以,动点M的轨迹C是以(0,0)为顶点,以(1,0)为焦点的抛物线,除去原点;
(2)设A(x1,y1),B(x2,y2),则
∵
 ,∴(1-x1,-y1)=2(x2-1,y2),
,∴(1-x1,-y1)=2(x2-1,y2),∴x1+2x2=3,y1=-2y2,
∵y12=4x1,y22=4x2,
∴x1=2,y1=±

∴直线L的方程为y=±2
 (x-1).
(x-1).点评:本题以向量得数量积得坐标表示为载体考查了轨迹方程,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足
已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足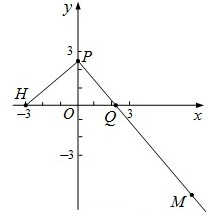 (2009•卢湾区二模)如图,已知点H(-3,0),动点P在y轴上,点Q在x轴上,其横坐标不小于零,点M在直线PQ上,且满足
(2009•卢湾区二模)如图,已知点H(-3,0),动点P在y轴上,点Q在x轴上,其横坐标不小于零,点M在直线PQ上,且满足